AT_arc205_d [ARC205D] Non-Ancestor Matching

给定一棵有 $N$ 个顶点的有根树，顶点编号为 $1$ 到 $N$。顶点 $1$ 是根节点，顶点 $i$ 的父节点为 $p_i$（$2 \le i \le N$，$1\le p_i < i$）。最初，所有顶点均被染为白色。 你可以执行如下操作任意多次（包括零次）： - 选择一对整数 $(u,v)$，满足以下所有条件： - $1\le u < v \le N$ - 顶点 $u$ 和 $v$ 都是白色。 - $u$ 不是 $v$ 的祖先。 - 将顶点 $u$ 和 $v$ 染为黑色。 这里，$u$ 不是 $v$ 的祖先，表示无论你对 $v$ 向上传递到父节点多少次，都无法到达 $u$。 请你在合适的操作顺序下，计算你最多可以执行多少次操作。 有 $T$ 组测试数据，请你求出每组的答案。

输入按如下格式给出： > $T$ > > $\text{case}_1$ > > $\text{case}_2$ > > $\vdots$ > > $\text{case}_T$ 每组测试数据 $\text{case}_i$ 格式如下： > $N$ > > $p_2$ $p_3$ $\ldots$ $p_N$

输出 $T$ 行。 第 $i$ 行（$1\le i\le T$）输出第 $i$ 个测试用例的答案。

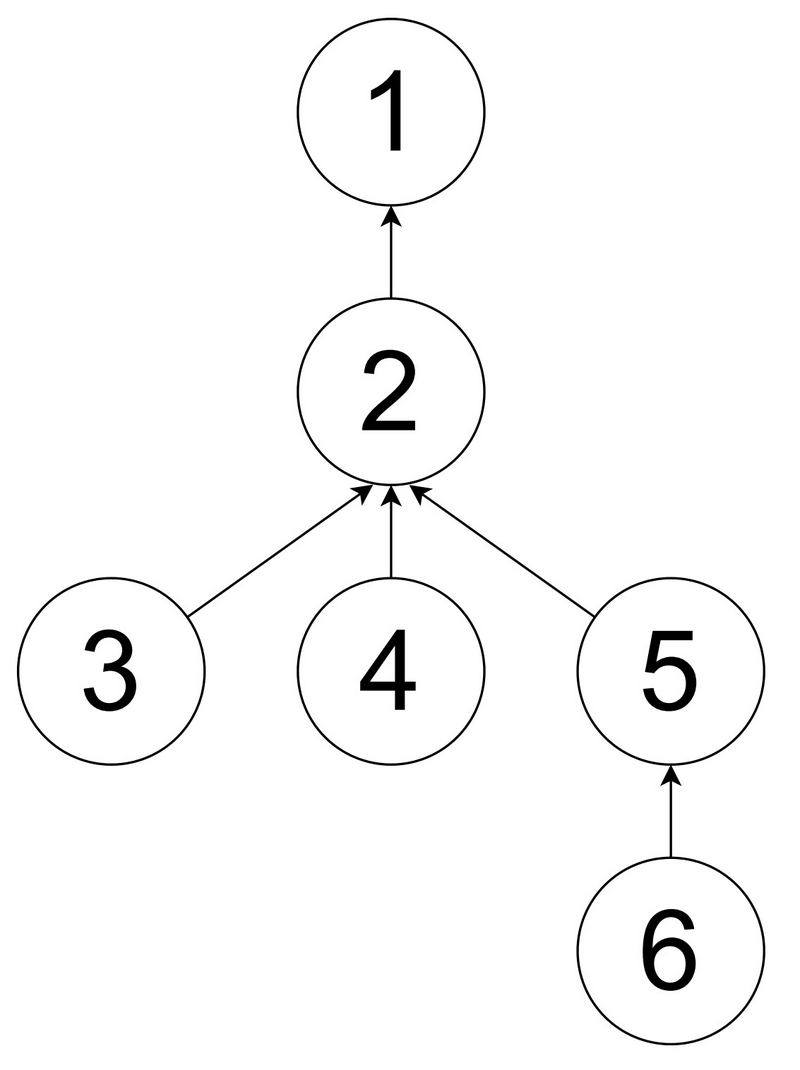
### 示例解释 1 考虑第一个测试用例。  你可以如下进行两次操作： - 选择 $(u,v)=(3,5)$，将顶点 $3$ 和 $5$ 染成黑色。 - 选择 $(u,v)=(4,6)$，将顶点 $4$ 和 $6$ 染成黑色。 无法进行超过两次的操作，因此第一行输出 $2$。 ### 数据范围 - $1\le T\le 5\times 10^4$ - $2\le N\le 5\times 10^5$ - $1\le p_i < i$ - 所有测试用例的 $N$ 之和不超过 $5\times 10^5$。 - 所有输入值均为整数。 由 ChatGPT 5 翻译