AT_arc206_e [ARC206E] Rectangle Coloring

有一个 $N\times N$ 的棋盘，其中 $N$ 至少为 $4$。棋盘最外层边界上但不在四个角上的格子称为好格子。更正式地说，对于 $1\leq i,j \leq N$，且 $i=1$ 或 $i=N$ 或 $j=1$ 或 $j=N$ 的格子，去除四个角格 $(1,1),(1,N),(N,1),(N,N)$ 后，剩下的格子被称为好格子。这里 $(r,c)$ 表示第 $r$ 行第 $c$ 列的格子。 每个好格子上写有一个整数。这些信息通过长度为 $N-2$ 的四个整数数列给出：$U=(U_1,\ldots,U_{N-2})$、$D=(D_1,\ldots,D_{N-2})$、$L=(L_1,\ldots,L_{N-2})$、$R=(R_1,\ldots,R_{N-2})$。 这四个数列的每个元素与好格子的对应关系如下： - $U_i$ ：对应 $(1,i+1)$ - $D_i$ ：对应 $(N,i+1)$ - $L_i$ ：对应 $(i+1,1)$ - $R_i$ ：对应 $(i+1,N)$ 此外，棋盘上所有格子初始均为白色。你可以进行如下操作任意次数： - 每次选择两个未被选择过的好格子，分别记为 $(r_1,c_1)$ 和 $(r_2,c_2)$。然后将满足 $\min(r_1,r_2)\leq i \leq \max(r_1,r_2)$ 且 $\min(c_1,c_2)\leq j \leq \max(c_1,c_2)$ 的所有格子染成黑色。每次操作的代价等于所选两好格子上整数之和。 请你计算将所有格子全部染黑所需的最小总代价。 对于 $T$ 组测试数据，分别输出答案。

输入由标准输入给出，格式如下： > $T$ $\mathrm{case}_1$ $\vdots$ $\mathrm{case}_T$ 每组测试数据格式如下： > $N$ $U_1$ ... $U_{N-2}$ $D_1$ ... $D_{N-2}$ $L_1$ ... $L_{N-2}$ $R_1$ ... $R_{N-2}$

输出 $T$ 行。 第 $i$ 行输出第 $i$ 组测试数据的答案。

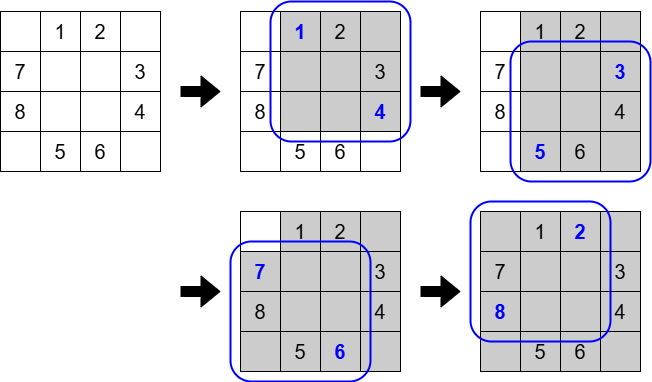
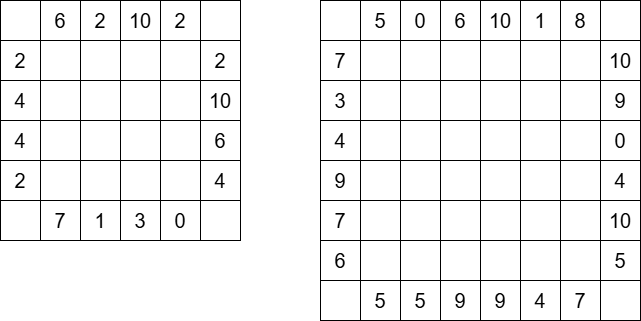
### 样例解释 1 在第 $1$ 组测试数据中，可以按如下方式染黑所有格子： - 选择 $(1,2)$ 和 $(3,4)$ 染色； - 选择 $(2,4)$ 和 $(4,2)$ 染色； - 选择 $(4,3)$ 和 $(2,1)$ 染色； - 选择 $(3,1)$ 和 $(1,3)$ 染色。 总代价为 $(1+4)+(3+5)+(6+7)+(8+2)=36$。  第 $2$、$3$ 组测试数据的棋盘如下图所示：  ### 数据范围 - 所有输入均为整数。 - $1 \leq T \leq 12500$ - $4 \leq N \leq 5\times 10^4$ - $0\leq U_i,D_i,L_i,R_i \leq 10^9$ - 所有测试数据的 $N$ 之和不超过 $5\times 10^4$。 由 ChatGPT 5 翻译