AT_arc206_e [ARC206E] Rectangle Coloring

There is an $ N\times N $ board, where $ N $ is at least $ 4 $ . The cells on the outermost edge of the board that are not corners are called good cells. More formally, among $ (i,j) $ such that $ 1\leq i,j \leq N $ and $ i=1 $ or $ i=N $ or $ j=1 $ or $ j=N $ , the cells excluding $ (1,1),(1,N),(N,1),(N,N) $ are called good cells. Here, $ (r,c) $ refers to the cell in row $ r $ and column $ c $ . All good cells have integers written on them. This information is given as four integer sequences of length $ N-2 $ : $ U=(U_1,\ldots,U_{N-2}),D=(D_1,\ldots,D_{N-2}),L=(L_1,\ldots,L_{N-2}),R=(R_1,\ldots,R_{N-2}) $ . Each element of these integer sequences corresponds to the integer written on a good cell as follows: - $ U_i $ : $ (1,i+1) $ - $ D_i $ : $ (N,i+1) $ - $ L_i $ : $ (i+1,1) $ - $ R_i $ : $ (i+1,N) $ Also, all cells on the board are initially colored white. You can perform the following operation any number of times: - Choose two good cells that have never been chosen in any previous operation. Let the two chosen good cells be $ (r_1,c_1) $ and $ (r_2,c_2) $ . For all $ (i,j) $ satisfying $ \min(r_1,r_2)\leq i \leq \max(r_1,r_2) $ and $ \min(c_1,c_2)\leq j \leq \max(c_1,c_2) $ , color $ (i,j) $ black. The cost of the operation is the sum of the integers written on the two chosen good cells. Find the minimum total cost required to color all cells black. Answer for $ T $ test cases.

The input is given from Standard Input in the following format: > $ T $ $ \mathrm{case}_1 $ $ \vdots $ $ \mathrm{case}_T $ Each test case is given in the following format: > $ N $ $ U_1 $ $ \ldots $ $ U_{N-2} $ $ D_1 $ $ \ldots $ $ D_{N-2} $ $ L_1 $ $ \ldots $ $ L_{N-2} $ $ R_1 $ $ \ldots $ $ R_{N-2} $

Output $ T $ lines. For the $ i $ -th line, output the answer for the $ i $ -th test case.

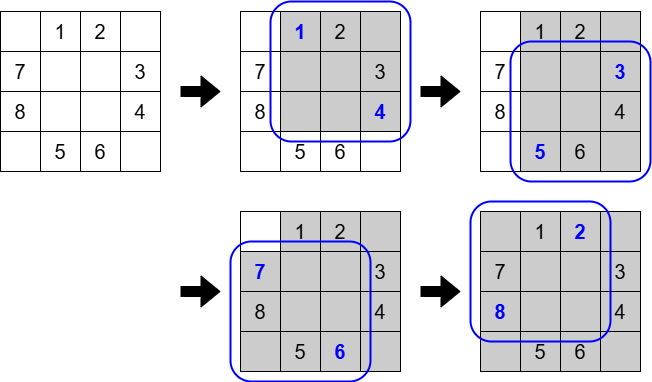
### Sample Explanation 1 In the $ 1 $ -st test case, you can color all cells black as follows: - Perform the operation choosing $ (1,2) $ and $ (3,4) $ . - Perform the operation choosing $ (2,4) $ and $ (4,2) $ . - Perform the operation choosing $ (4,3) $ and $ (2,1) $ . - Perform the operation choosing $ (3,1) $ and $ (1,3) $ . The total cost is $ (1+4)+(3+5)+(6+7)+(8+2)=36 $ .  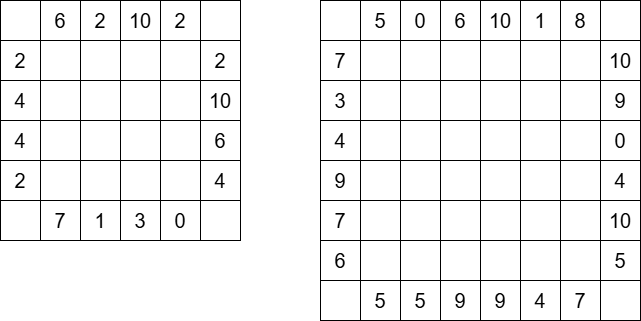For the $ 2 $ -nd and $ 3 $ -rd test cases, the input boards are illustrated below:  ### Constraints - All input values are integers. - $ 1 \leq T \leq 12500 $ - $ 4 \leq N \leq 5\times 10^4 $ - $ 0\leq U_i,D_i,L_i,R_i \leq 10^9 $ - The sum of $ N $ over all test cases does not exceed $ 5\times 10^4 $ .