AT_arc206_e [ARC206E] Rectangle Coloring

$ N\times N $ の盤面があります．ここで $ N $ は $ 4 $ 以上です．盤面の最も外側かつ角でないマスを，良いマスと呼びます．より厳密には， $ 1\leq i,j \leq N $ であって， $ i=1 $ または $ i=N $ または $ j=1 $ または $ j=N $ であるような $ (i,j) $ のうち， $ (1,1),(1,N),(N,1),(N,N) $ を除いたマスを良いマスと呼びます．ここで， $ (r,c) $ は $ r $ 行 $ c $ 列目のマスを指します． 全ての良いマスには整数が書いてあります．この情報は， $ 4 $ 個の長さ $ N-2 $ の整数列 $ U=(U_1,\ldots,U_{N-2}),D=(D_1,\ldots,D_{N-2}),L=(L_1,\ldots,L_{N-2}),R=(R_1,\ldots,R_{N-2}) $ として与えられます． この整数列の各要素は，以下のように良いマスに書かれた整数と対応しています． - $ U_i $ ： $ (1,i+1) $ - $ D_i $ ： $ (N,i+1) $ - $ L_i $ ： $ (i+1,1) $ - $ R_i $ ： $ (i+1,N) $ また，盤面の全てのマスは初め白色で塗られています．あなたは以下の操作を何回でも行えます． - これまでの操作で一度も選ばれていない良いマスを二つ選ぶ．選んだ二つの良いマスを $ (r_1,c_1) $ と $ (r_2,c_2) $ として， $ \min(r_1,r_2)\leq i \leq \max(r_1,r_2) $ かつ $ \min(c_1,c_2)\leq j \leq \max(c_1,c_2) $ を満たす全ての $ (i,j) $ に対して， $ (i,j) $ を黒く塗る． 操作にかかるコストは選んだ二つの良いマスに書かれている整数の和である． 全てのマスを黒くするために必要なコストの総和の最小値を求めてください． $ T $ 個のテストケースについて答えてください．

入力は以下の形式で標準入力から与えられる． > $ T $ $ \mathrm{case}_1 $ $ \vdots $ $ \mathrm{case}_T $ 各テストケースは以下の形式で与えられる． > $ N $ $ U_1 $ $ \ldots $ $ U_{N-2} $ $ D_1 $ $ \ldots $ $ D_{N-2} $ $ L_1 $ $ \ldots $ $ L_{N-2} $ $ R_1 $ $ \ldots $ $ R_{N-2} $

$ T $ 行出力せよ． $ i $ 行目には， $ i $ 番目のテストケースの答えを出力せよ．

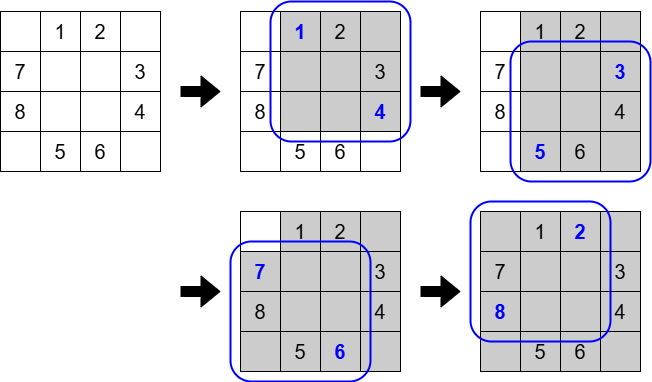
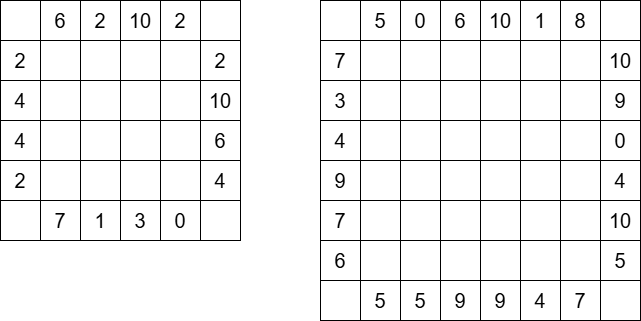
### Sample Explanation 1 $ 1 $ 番目のテストケースでは， - $ (1,2) $ と $ (3,4) $ を選んで操作 - $ (2,4) $ と $ (4,2) $ を選んで操作 - $ (4,3) $ と $ (2,1) $ を選んで操作 - $ (3,1) $ と $ (1,3) $ を選んで操作 とすると，全てのマスを黒くすることができます．コストの総和は， $ (1+4)+(3+5)+(6+7)+(8+2)=36 $ です．  $ 2 $ 番目， $ 3 $ 番目のテストケースについて，入力される盤面を図示すると次のようになります．  ### Constraints - 入力される数値は全て整数 - $ 1 \leq T \leq 12500 $ - $ 4 \leq N \leq 5\times 10^4 $ - $ 0\leq U_i,D_i,L_i,R_i \leq 10^9 $ - 全てのテストケースにわたる $ N $ の総和は $ 5\times 10^4 $ を超えない