AT_arc210_d [ARC210D] Independent Set Game

You are given a simple undirected graph $ G $ with $ N $ vertices and $ M $ edges, where vertices are numbered $ 1 $ to $ N $ . The $ i $ -th edge connects vertices $ u_i $ and $ v_i $ . Initially, no vertices of $ G $ are colored. Alice and Bob will play a game using $ G $ . Alice and Bob perform the following actions in order for $ t=1,\ldots,N $ : - If $ t $ is odd, Alice chooses one vertex that is not yet colored and colors that vertex black. - If $ t $ is even, Bob chooses one vertex that is not yet colored and colors that vertex white. After all $ N $ actions are completed, if the set of all vertices colored black is an independent set of $ G $ , Alice is the winner; otherwise, Bob is the winner. Output the name of the winner when both players play optimally. You are given $ T $ test cases; solve each of them. What is an independent setA set $ S $ consisting of vertices of a simple undirected graph $ G $ is an independent set of $ G $ if there does not exist a pair of vertices $ u $ and $ v $ connected by an edge such that $ u\in S $ and $ v\in S $ .

The input is given from Standard Input in the following format: > $ T $ $ \mathrm{case}_1 $ $ \mathrm{case}_2 $ $ \vdots $ $ \mathrm{case}_T $ Each case is given in the following format: > $ N $ $ M $ $ u_1 $ $ v_1 $ $ \vdots $ $ u_M $ $ v_M $

Output $ T $ lines. The $ i $ -th line should contain the name of the winner (`Alice` or `Bob`) for the $ i $ -th test case when both players play optimally.

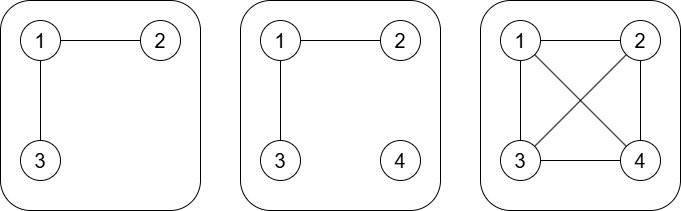
### Sample Explanation 1 The graph given in each test case is illustrated below:  ### Constraints - $ 1\leq T\leq 2\times 10^5 $ - $ 2\leq N\leq 2\times 10^5 $ - $ 0\leq M\leq 2\times 10^5 $ - $ 1\leq u_i < v_i \leq N $ - The given graph is a simple undirected graph. - The sum of $ N $ over all test cases is at most $ 2\times 10^5 $ . - The sum of $ M $ over all test cases is at most $ 2\times 10^5 $ .