AT_arc210_d [ARC210D] Independent Set Game

给定一张简单无向图 $G$，包含 $N$ 个顶点和 $M$ 条边，顶点编号为 $1$ 到 $N$。第 $i$ 条边连接顶点 $u_i$ 与 $v_i$。 一开始，$G$ 上所有顶点都没有被染色。Alice 和 Bob 将在 $G$ 上玩一个游戏，具体规则如下：对于 $t=1,\ldots,N$： - 如果 $t$ 是奇数，Alice 从尚未染色的顶点中选择一个，把该顶点染成黑色。 - 如果 $t$ 是偶数，Bob 从尚未染色的顶点中选择一个，把该顶点染成白色。 所有 $N$ 次操作完成后，如果所有被染成黑色的顶点构成 $G$ 的一个独立集，则 Alice 获胜；否则，Bob 获胜。当双方都采取最优策略时，请输出最后的获胜者名字。 你需要完成 $T$ 组测试，对于每组，输出胜者名字。 什么是独立集？ 在一张简单无向图 $G$ 中，顶点集 $S$ 是 $G$ 的独立集，如果不存在一对通过边直接相连的顶点 $u,v$ 满足 $u\in S$ 且 $v\in S$。

输入采用如下格式： > $T$ > > $\mathrm{case}_1$ > > $\mathrm{case}_2$ > > $\vdots$ > > $\mathrm{case}_T$ 每组测试输入如下： > $N$ $M$ > > $u_1$ $v_1$ > > $\vdots$ > > $u_M$ $v_M$

输出共 $T$ 行，第 $i$ 行为第 $i$ 组测试在双方均最优策略下胜者的名字（`Alice` 或 `Bob`）。

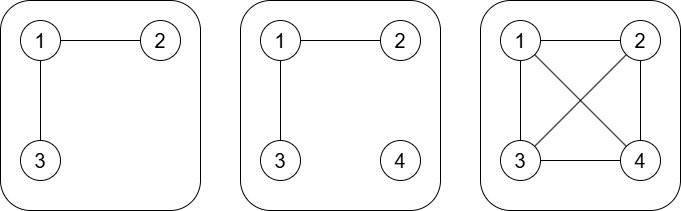
### 样例解释 1 每组样例中的图示如下：  ### 数据范围 - $1 \leq T \leq 2 \times 10^5$ - $2 \leq N \leq 2 \times 10^5$ - $0 \leq M \leq 2 \times 10^5$ - $1 \leq u_i < v_i \leq N$ - 给定的图是简单无向图。 - 所有测试用例中 $N$ 的总和不超过 $2 \times 10^5$。 - 所有测试用例中 $M$ 的总和不超过 $2 \times 10^5$。 由 ChatGPT 5 翻译