AT_arc211_d [ARC211D] Michishirube

给定一个有 $N$ 个顶点和 $M$ 条边的简单连通无向图。第 $i$ 条边 $(1\leq i\leq M)$ 为无向边，连接顶点 $U_i$ 和 $V_i$。 请按如下规定在所有顶点上放置指示牌： - 除顶点 $1$ 外，每个顶点放置一个蓝色指示牌，指向它的一个相邻顶点。 - 除顶点 $2$ 外，每个顶点放置一个黄色指示牌，指向它的一个相邻顶点。 同一顶点的两个指示牌指向的顶点不能是同一个。 判断是否存在一种指示牌的放置方式，使得满足以下条件，如果存在，输出其中一种方案： - 从除顶点 $1$ 外的任意一个顶点出发，无限次沿着蓝色指示牌指向的顶点前进，最终必然到达顶点 $1$。 - 从除顶点 $2$ 外的任意一个顶点出发，无限次沿着黄色指示牌指向的顶点前进，最终必然到达顶点 $2$。 如果存在多种满足条件的放置方式，你可以输出其中任意一种。

输入以如下格式从标准输入给出： > $N$ $M$ $U_1$ $V_1$ $U_2$ $V_2$ > $\vdots$ > $U_M$ $V_M$

如果不存在满足条件的放置方法，只需输出一行 `No`。 如果存在，输出 $N+1$ 行。 第一行输出 `Yes`。 第二行输出顶点 $1$ 上黄色指示牌指向的顶点的编号。 第三行输出顶点 $2$ 上蓝色指示牌指向的顶点的编号。 第 $i$ 行（$4\leq i\leq N+1$）输出两个用空格分隔的整数，分别为顶点 $i-1$ 上蓝色指示牌指向的顶点的编号，以及黄色指示牌指向的顶点的编号。 如果存在多种方案，你可以输出其中任意一种。

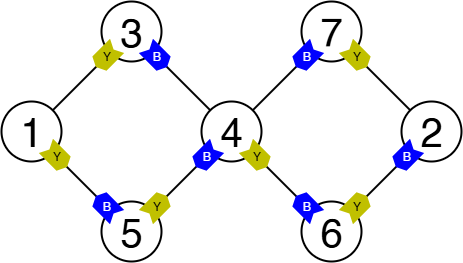
### 样例解释 1 此处指示牌的放置方式如图所示。例如，从顶点 $3$ 出发： - 遵循蓝色指示牌前进，路径为 $3\rightarrow 4\rightarrow 5\rightarrow 1$，最终到达顶点 $1$。 - 遵循黄色指示牌前进，路径为 $3\rightarrow 1\rightarrow 5\rightarrow 4\rightarrow 6\rightarrow 2$，最终到达顶点 $2$。 同样可以验证，从顶点 $2$ 遵循蓝色指示牌也可以到达 $1$，从顶点 $1$ 遵循黄色指示牌也可以到达 $2$，其他顶点也都满足条件。  虽然存在多种方案，但例如顶点 $3$ 上的蓝色指示牌和黄色指示牌都不能指向顶点 $4$，因为同一顶点两个指示牌不允许指向同一个顶点。 ### 样例解释 2 不存在满足条件的指示牌放置方式。 ### 约束条件 - $2\leq N\leq 2\times 10^5$ - $1\leq M\leq 3\times 10^5$ - $1\leq U_i < V_i\leq N$ 且 $1\leq i\leq M$ - 给定图保证简单且连通。 - 所有输入都是整数。 由 ChatGPT 5 翻译