AT_arc211_d [ARC211D] Michishirube

You are given a simple connected undirected graph with $ N $ vertices and $ M $ edges. The $ i $ -th edge $ (1\leq i\leq M) $ is an undirected edge connecting vertices $ U_i $ and $ V_i $ . Place signposts at all vertices as follows: - At every vertex except vertex $ 1 $ , place a blue signpost pointing to one of its adjacent vertices. - At every vertex except vertex $ 2 $ , place a yellow signpost pointing to one of its adjacent vertices. Here, the two signposts at the same vertex must not point to the same vertex. Determine whether it is possible to place signposts satisfying the following conditions, and if possible, output one way to place them: - From any vertex other than vertex $ 1 $ , you can reach vertex $ 1 $ by repeatedly moving to the vertex pointed to by the blue signpost a finite number of times. - From any vertex other than vertex $ 2 $ , you can reach vertex $ 2 $ by repeatedly moving to the vertex pointed to by the yellow signpost a finite number of times. If there are multiple ways to place signposts satisfying the conditions, you may output any of them.

The input is given from Standard Input in the following format: > $ N $ $ M $ $ U_1 $ $ V_1 $ $ U_2 $ $ V_2 $ $ \vdots $ $ U_M $ $ V_M $

If there is no way to place signposts satisfying the conditions, output `No` only. If there is, output $ N+1 $ lines. The first line should contain `Yes`. The second line should contain the number of the vertex pointed to by the yellow signpost at vertex $ 1 $ . The third line should contain the number of the vertex pointed to by the blue signpost at vertex $ 2 $ . The $ i $ -th line $ (4\leq i\leq N+1) $ should contain the number of the vertex pointed to by the blue signpost at vertex $ i-1 $ and the number of the vertex pointed to by the yellow signpost at vertex $ i-1 $ , in this order, separated by a space. If there are multiple solutions, you may output any of them.

### Sample Explanation 1 Here, signposts are placed as shown in the figure below. For example, from vertex $ 3 $ : - Following the blue signpost, you move as vertex $ 3\rightarrow 4\rightarrow 5\rightarrow 1 $ , eventually reaching vertex $ 1 $ . - Following the yellow signpost, you move as vertex $ 3\rightarrow 1\rightarrow 5\rightarrow 4 \rightarrow 6\rightarrow 2 $ , eventually reaching vertex $ 2 $ . You can also verify that following the blue signpost from vertex $ 2 $ leads to vertex $ 1 $ , and following the yellow signpost from vertex $ 1 $ leads to vertex $ 2 $ . The other vertices also satisfy the conditions.  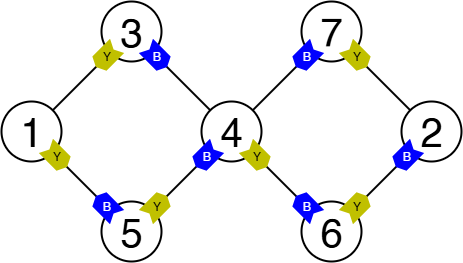There are multiple other solutions, but you must not have both the blue signpost and the yellow signpost at vertex $ 3 $ point to vertex $ 4 $ , because the signposts at the same vertex would point to the same vertex. ### Sample Explanation 2 There is no way to place signposts satisfying the conditions. ### Constraints - $ 2\leq N\leq 2\times 10^5 $ - $ 1\leq M\leq 3\times 10^5 $ - $ 1\leq U_i\lt V_i\leq N $ $ (1\leq i\leq M) $ - The given graph is simple and connected. - All input values are integers.