AT_arc211_d [ARC211D] Michishirube

$ N $ 頂点 $ M $ 辺の単純連結無向グラフが与えられます。 $ i $ 番目 $ (1\leq i\leq M) $ の辺は頂点 $ U_i $ と頂点 $ V_i $ を結ぶ無向辺です。 すべての頂点に、以下のように道標を立てます。 - 頂点 $ 1 $ 以外のすべての頂点に、隣接している頂点のうちどれか $ 1 $ つを指す青色の道標を立てる。 - 頂点 $ 2 $ 以外のすべての頂点に、隣接している頂点のうちどれか $ 1 $ つを指す黄色の道標を立てる。 ただし、同じ頂点にある $ 2 $ つの道標が同じ頂点を指してはいけません。 以下の条件を満たすように道標を立てることは可能か判定し、可能なら道標の立て方を $ 1 $ つ出力してください。 - 頂点 $ 1 $ 以外のどの頂点からも、青色の道標の指す頂点に動くことを有限回繰り返すことで頂点 $ 1 $ に到達することができる。 - 頂点 $ 2 $ 以外のどの頂点からも、黄色の道標の指す頂点に動くことを有限回繰り返すことで頂点 $ 2 $ に到達することができる。 条件を満たす道標の立て方が複数ある場合、どれを出力してもかまいません。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ U_1 $ $ V_1 $ $ U_2 $ $ V_2 $ $ \vdots $ $ U_M $ $ V_M $

条件を満たす道標の立て方が存在しない場合、`No` とだけ出力せよ。 存在する場合、 $ N+1 $ 行出力せよ。 $ 1 $ 行目には、`Yes` と出力せよ。 $ 2 $ 行目には、頂点 $ 1 $ に立てる黄色の道標が指す頂点の番号を出力せよ。 $ 3 $ 行目には、頂点 $ 2 $ に立てる青色の道標が指す頂点の番号を出力せよ。 $ i $ 行目 $ (4\leq i\leq N+1) $ には、頂点 $ i-1 $ に立てる青色の道標が指す頂点の番号、黄色の道標が指す頂点の番号をこの順に空白区切りで出力せよ。 解が複数ある場合、どれを出力してもかまわない。

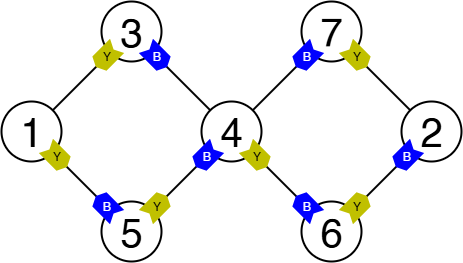
### Sample Explanation 1 下図のような道標の立て方です。たとえば、頂点 $ 3 $ からは - 青色の道標に沿うと、頂点 $ 3\rightarrow 4\rightarrow 5\rightarrow 1 $ と動き、最終的に頂点 $ 1 $ に到達します。 - 黄色の道標に沿うと、頂点 $ 3\rightarrow 1\rightarrow 5\rightarrow 4 \rightarrow 6\rightarrow 2 $ と動き、最終的に頂点 $ 2 $ に到達します。 また、頂点 $ 2 $ から青色の道標に沿って移動すると頂点 $ 1 $ に到達できること、頂点 $ 1 $ から黄色の道標に沿って移動すると頂点 $ 2 $ に到達できることも確かめることができます。その他の頂点も条件を満たします。  この他にも複数の解がありますが、頂点 $ 3 $ にある青色の道標と黄色の道標をともに頂点 $ 4 $ に向けてはいけません。同じ頂点にある道標が同じ頂点を指してしまうためです。 ### Sample Explanation 2 条件を満たす道標の立て方は存在しません。 ### Constraints - $ 2\leq N\leq 2\times 10^5 $ - $ 1\leq M\leq 3\times 10^5 $ - $ 1\leq U_i\lt V_i\leq N $ $ (1\leq i\leq M) $ - 与えられるグラフは単純かつ連結 - 入力はすべて整数