AT_atcoder11live_a Turn Right

AtCoder社の高橋社長はオフィスで車のおもちゃを走らせて遊んでいる。 このおもちゃは障害物にぶつかるまで真っ直ぐ動き、障害物にぶつかると右に90度向きを変える、という動作を延々と繰り返す。 この動作を繰り返していると、そのうち既に通ったことのある場所を同じ向きで通過し、そこから先は同じルートをぐるぐると無限ループすることになる。 高橋社長は車は大好きだが無限ループは大嫌いなため、オフィスに障害物を設置することで、無限ループするまでに出来るだけ長い距離を移動出来るようなコースを作成することにした。 高橋社長の手伝いをして欲しい。 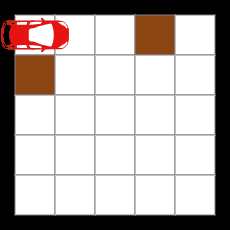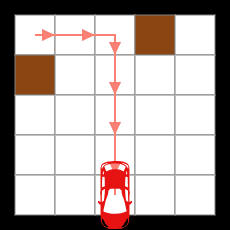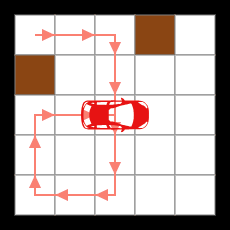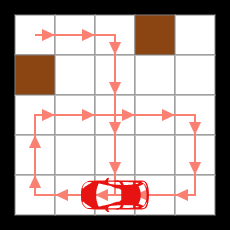 無限ループするまでの移動例 (無限ループに突入するまでの移動距離18)

有一个 $n \times n$ 的棋盘。最左上方的格子的坐标为 $(0, 0)$，从该处向下走 $i$ 格，向右走 $j$ 格时，所在格子的坐标为 $(i, j)$。初始状态下，一个玩具车以右向状态被放置在 $(si, sj)$ 位置。 在若干格子上初始已放置有障碍物，这些障碍物无法移除，也不能移动到其他格子上。同时，$n \times n$ 范围外的所有格子都视为有障碍物。请在剩余的空白格内，随意布置新的障碍物。但保证玩具车的初始位置没有障碍物，也不能在该位置新放障碍物。 障碍物的布置完成后，玩具车会按如下规则移动： 1. 如果当前方向前方一格有障碍物，则原地右转 $90$°。 2. 如果当前方向前方一格无障碍物，则向前移动一格。 不断重复上述动作后，玩具车最终会以同样的位置和方向再次经过已访问过的格子，从此进入死循环。在进入死循环前，移动的距离尽量长。此处「进入死循环前的移动距离」指的是第一次到达之前以相同位置和方向出现的状态时，之前依照规则2执行的次数（若最后一步为规则2，也要计入）。

输入通过标准输入给出，格式如下： > $n$ $si$ $sj$ $b_0$ $⋮$ $b_{n-1}$ $n$ 表示棋盘的大小，是一个 $20$ 到 $50$ 之间的整数。$(si, sj)$ 表示玩具车的初始位置，是两个 $0$ 到 $n-1$ 的整数。每个 $b_i$ 是由 `#` 和 `.` 构成的长度为 $n$ 的字符串，其中第 $j$ 个字符（$0 \leq j \leq n-1$），若 $(i, j)$ 处有障碍物则为 `#`，否则为 `.`。

设新放的障碍物总数为 $m$，放置在 $(i_0, j_0), \cdots, (i_{m-1}, j_{m-1})$ 这些位置。按下述格式输出至标准输出： > $m$ $i_0$ $j_0$ $⋮$ $i_{m-1}$ $j_{m-1}$ 不能在同一格放多个障碍物，玩具车起始位置格子也不得放置任何障碍物。如果不满足这些条件，评测结果会被判为 WA。 [查看样例](https://img.atcoder.jp/atcoder11live/f62fc84.html?lang=ja&seed=0&output=31%0D%0A19+19%0D%0A18+7%0D%0A2+9%0D%0A16+0%0D%0A17+18%0D%0A19+9%0D%0A0+12%0D%0A16+11%0D%0A13+0%0D%0A14+18%0D%0A16+17%0D%0A15+12%0D%0A11+13%0D%0A12+18%0D%0A13+17%0D%0A8+0%0D%0A9+7%0D%0A11+6%0D%0A10+1%0D%0A6+2%0D%0A9+18%0D%0A3+1%0D%0A0+5%0D%0A6+4%0D%0A5+2%0D%0A2+3%0D%0A3+17%0D%0A6+16%0D%0A5+12%0D%0A3+19%0D%0A2+14%0D%0A)

## 得分 令进入死循环前的移动距离为 $L$，初始空格总数为 $E$，则得分为 \[ \mathrm{round}\left(10^6\times\frac{L}{4 E}\right) \] 请实现一个放置障碍物的程序以尽力获得高分。 测试用例一共有 $100$ 个，各测试用例的得分总和为提交的总得分。第 $i=1,2,\cdots,100$ 个输入满足 $n=20 + \mathrm{floor}(31 \times (i-1)/100)$。如果有任意一个测试用例输出不合法或超时，总体会被判为 WA 或 TLE。最终排名由比赛期间获得的最高分决定，赛后不会有系统测试。得分相同时，排名不受提交时间影响。 ## 输入生成方法 用 $\mathrm{rand\_int}(L,U)$ 表示均匀生成 $L$ 到 $U$ 的整数，用 $\mathrm{rand\_double}(L,U)$ 表示均匀生成 $L$ 到 $U$ 之间的实数。 棋盘大小 $n$ 由 $\mathrm{rand\_int}(20,50)$ 生成。玩具车初始位置 $si=\mathrm{rand\_int}(0,n-1)$，$sj=\mathrm{rand\_int}(0,n-1)$。 概率 $p$ 从 $\mathrm{rand\_double}(0.01,0.1)$ 中随机选取，对除玩具车初始位置外的每个格子，以概率 $p$ 放置障碍物。 ## 工具（输入生成器、可视化工具） - [Web 版](https://img.atcoder.jp/atcoder11live/f62fc84.html?lang=ja)：比本地版更强，可动画显示与手动操作。 - [本地版](https://img.atcoder.jp/atcoder11live/f62fc84.zip)：需 [Rust 语言](https://www.rust-lang.org/ja) 编译环境。 - [Windows 版编译好的可执行文件](https://img.atcoder.jp/atcoder11live/f62fc84_windows.zip)：如果懒得配置 Rust 环境可直接用此。 由 ChatGPT 5 翻译