AT_cf17_final_i Full Tournament

有 $2^N$ 名选手进行了一场锦标赛。每位选手都有 $1$ 到 $2^N$ 的编号，当两名选手对战时，编号较小的选手一定获胜。 本次锦标赛有些不同，失败者之间也会进行比赛，从而确定所有选手的最终排名。 在这里，我们将这样的 $2^n$ 人比赛称为“等级为 $n$ 的全锦标赛”。等级为 $n$ 的全锦标赛的排名按照如下规则决定： - 等级为 $0$ 的全锦标赛只有 $1$ 名参与者，该选手获得第 $1$ 名。 - 等级为 $n\ (1 \leq n)$ 的全锦标赛，从 $2^n$ 名选手按顺序排成一行开始，排名的决定方式如下： - 首先，从一端开始，每两人分为一组，得到 $2^{n-1}$ 组，每组 $2$ 人。 - 每组进行对战，获胜者进入胜者组，失败者进入败者组。 - 将胜者组内的选手按原排列顺序重新排队，以此进行等级为 $n-1$ 的全锦标赛，决定他们的排名。 - 败者组也同样排序，但在他们的每个排名基础上加上 $2^{n-1}$。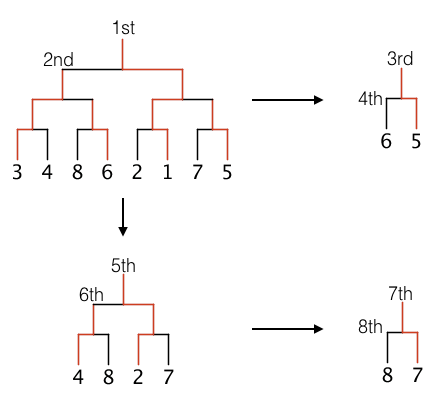 例如，将 $8$ 名选手按 $3,4,8,6,2,1,7,5$ 的顺序进行等级为 $3$ 的全锦标赛。比赛如图所示，最终按名次排列后的顺序为 $1,3,5,6,2,4,7,8$。  高桥君手中有一张记录着选手编号按锦标赛最终名次排列的纸条，但有些地方被弄脏无法辨认。现在给定这张纸的信息为长度为 $2^N$ 的数列 $A$，当 $A_i \geq 1$ 时，表示第 $i$ 名选手的编号为 $A_i$，当 $A_i = 0$ 时，表示第 $i$ 名选手的编号已不可辨认。 请判断是否存在一种初始选手排列顺序，通过这样的锦标赛最终结果能得到给定的名次序列 $A$。如果存在，请给出一种可能的初始排列。

输入以如下格式通过标准输入给出。 > $N$ $A_1$ $A_2$ $\cdots$ $A_{2^N}$

如果存在一种初始的选手排列顺序能够得到给定的名次序列，则输出 `YES`，第二行输出一种符合要求的初始排列，选手编号按顺序以空格分隔。 如果不存在，则输出 `NO`。

## 限制 - $1 \leq N \leq 18$ - $0 \leq A_i \leq 2^N$ - 除 $0$ 外，$A_i$ 中的整数不会重复出现。 ## 样例解释 1 与题目描述中的例子排列顺序相同。 由 ChatGPT 5 翻译