AT_cf17_final_i Full Tournament

[problemUrl]: https://atcoder.jp/contests/cf17-final/tasks/cf17_final_i $ 2^N $ 人の選手でトーナメント戦を行いました。 各選手には $ 1 $ 〜 $ 2^N $ の番号がついており、$ 2 $ 人が対戦したときは番号が小さい方の選手が必ず勝ちます。 行ったトーナメント戦は少し変わっていて、敗者どうしも対戦をすることで全員の順位を決めるものでした。 ここで、$ 2^n $ 人で行うこのようなトーナメント戦を「レベル $ n $ のフルトーナメント」と呼ぶことにします。 レベル $ n $ のフルトーナメントの順位は以下のように決定されます。 - レベル $ 0 $ のフルトーナメントでは参加者が $ 1 $ 人であり、この人が $ 1 $ 位となる。 - レベル $ n\ (1\ \leq\ n) $ のフルトーナメントは、$ 2^n $ 人の選手が横 $ 1 $ 列に並んだ状態から始まり、以下のように順位を決定する。 - まず、端から $ 2 $ 人ずつに区切り、$ 2^{n-1} $ 組の $ 2 $ 人組を作る。 - それぞれの $ 2 $ 人組で対戦を行い、勝った方が勝ちグループに、負けた方が負けグループに入る。 - 勝ちグループに入った選手を元の列での順序を保ったまま並べ、レベル $ n-1 $ のフルトーナメントを行い、各選手の順位を決定する。 - 負けグループについても同様に順位をつけ、その後に負けグループの各選手の順位に $ 2^{n-1} $ を足す。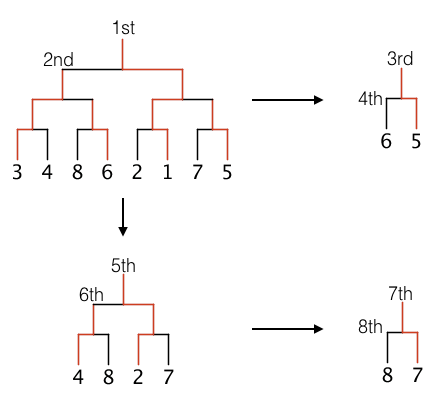 例えば、$ 8 $ 人の選手を $ 3,4,8,6,2,1,7,5 $ の順に並べてレベル $ 3 $ のフルトーナメントを行うと下図のようにトーナメントが行われ、結果の順位順に選手を並べると $ 1,3,5,6,2,4,7,8 $ となります。  高橋君は、選手の番号をトーナメントの結果の順位順に書いた紙を持っていましたが、いくつかの場所が汚れて読めなくなってしまいました。 この紙の情報は長さ $ N $ の数列 $ A $ として与えられ、$ A_i $ が $ 1 $ 以上のときは $ i $ 位の選手の番号が $ A_i $ であったことを表し、$ 0 $ のときは $ i $ 位の選手の番号が分からなくなってしまったことを表します。 最初の選手の並び順として考えられるものが存在するかどうかを判定し、存在するならば例を $ 1 $ つ答えてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ A_1 $ $ A_2 $ $ ... $ $ A_{2^N} $

最初の選手の並び順として考えられるものが存在する場合は `YES` と出力し、$ 2 $ 行目に選手の番号を順番に空白区切りで出力せよ。 存在しない場合は代わりに `NO` と出力せよ。

### 制約 - $ 1\ \leq\ N\ \leq\ 18 $ - $ 0\ \leq\ A_i\ \leq\ 2^N $ - $ A_i $ には $ 0 $ 以外の整数は重複して含まれていない。 ### Sample Explanation 1 問題文中の例と同じ並び順です。