AT_cf_2015_relay_f グラフの個数
题目描述
请分别求出对于 $N=3$ 到 $6$,顶点数和边数均为 $N$ 的无向连通图有多少种。要求图中不能有自环或重边,且顶点和边都不区分。
例如,当 $N=4$ 时,如下图所示,有 $2$ 种不同的图。
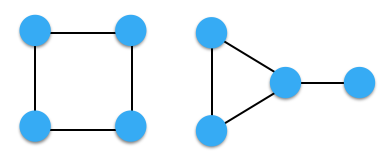
即使 $N$ 变大,能够构成的图也只能是**恰好包含 $1$ 个环**的图。
输入格式
本题没有输入。
输出格式
输出共 $4$ 行。
- 第 $1$ 行输出 $N=3$ 时的答案;
- 第 $2$ 行输出 $N=4$ 时的答案;
- 第 $3$ 行输出 $N=5$ 时的答案;
- 第 $4$ 行输出 $N=6$ 时的答案。
每行末尾需换行。
说明/提示
### 样例解释 1
$N=4$ 时的答案如题面所示。其他答案在题面中用 `?` 隐藏,照抄无法得分。
由 ChatGPT 4.1 翻译