AT_cf_2015_relay_f グラフの個数

[problemUrl]: https://atcoder.jp/contests/code-festival-2015-relay/tasks/cf_2015_relay_f 頂点の個数と辺の本数がどちらも $ N $ であるような、無向連結グラフが何種類あるかを $ N=3～6 $ についてそれぞれ求めてください。ただし、自己ループや多重辺があってはいけません。頂点どうしや辺どうしは区別しません。 例えば $ N=4 $ のときは、下図のような $ 2 $ 種類のグラフがあります。 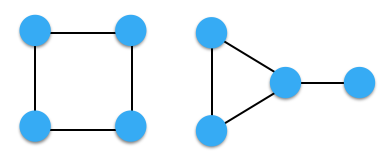 $ N $ が大きくなっても、出来るグラフは **サイクルがちょうど $ 1 $ つ含まれる** グラフになります。

この問題には入力はありません。

出力は $ 4 $ 行からなる。 - $ 1 $ 行目には、$ N=3 $ のときの答え - $ 2 $ 行目には、$ N=4 $ のときの答え - $ 3 $ 行目には、$ N=5 $ のときの答え - $ 4 $ 行目には、$ N=6 $ のときの答え をそれぞれ出力せよ。出力の末尾にも改行を入れること。

### Sample Explanation 1 $ N=4 $ のときの答えは問題文中のとおりです。ですが、それ以外の答えは `?` で隠してあるのでこのとおりに出力しても正解にはなりません。