AT_chokudai004_a Just Write Numbers!
题目描述
高桥君非常喜欢三个整数 $B_1, B_2, B_3$。为此,他计划在一个 $N \times N$ 的网格中填入数字,希望在这些数字的某些连续的横向或纵向区间中,能够找到和为他喜爱的那些数的区间。
例如,当高桥君钟爱的数字是 $13$ 时,如下图中红色标出的区间就是符合条件的。
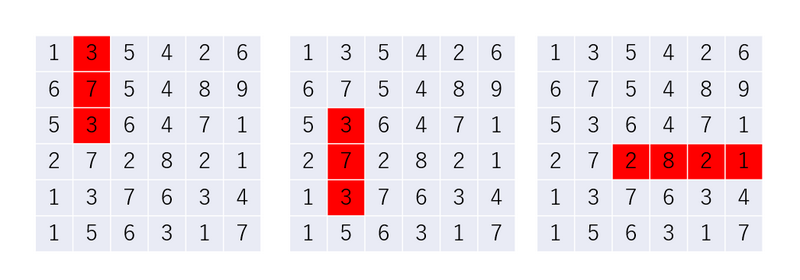
设和等于 $B_1, B_2, B_3$ 的连续区间的数量分别为 $A_1, A_2, A_3$,那么高桥君可以得到的总分数为 $A_1 \times B_1 + A_2 \times B_2 + A_3 \times B_3$。
不过,高桥君不能随心所欲地填写数字,因为每个格子都有一个规定的最小值和最大值。第 $i$ 行第 $j$ 列的格子只能填写在 $l_{i,j}$ 到 $r_{i,j}$ 之间的数字。
请帮高桥君找到一种填写数字的方法,使得他可以获得尽可能高的分数。
此题属于马拉松类型问题,不要求提交最优解。只要提交的解满足题目要求,就可以获得相应分数。
输入格式
输入提供如下信息:
> $N$ $B_1$ $B_2$ $B_3$ $l_{1,1}$ $l_{1,2}$ ... $l_{1,N}$ $l_{2,1}$ $l_{2,2}$ ... $l_{2,N}$ : $l_{N,1}$ $l_{N,2}$ ... $l_{N,N}$ $r_{1,1}$ $r_{1,2}$ ... $r_{1,N}$ $r_{2,1}$ $r_{2,2}$ ... $r_{2,N}$ : $r_{N,1}$ $r_{N,2}$ ... $r_{N,N}$
输出格式
输出每个格子的填入数字 $A_{i,j}$,格式如下:
> $A_{1,1}$ $A_{1,2}$ ... $A_{1,N}$ $A_{2,1}$ $A_{2,2}$ ... $A_{2,N}$ : $A_{N,1}$ $A_{N,2}$ ... $A_{N,N}$
所有输出的 $A_{i,j}$ 需满足 $l_{i,j} \leq A_{i,j} \leq r_{i,j}$ 才算是正确答案,从而根据题目规则获得分数。
如果输出不合法,几乎所有测试用例都会被判为 $0$ 分。
说明/提示
- 网格的大小 $N = 30$
- 高桥君喜欢的整数范围为 $10 \leq B_1 \leq 19$
- $20 \leq B_2 \leq 29$
- $30 \leq B_3 \leq 39$
- 每个格子内的最小值和最大值范围为 $1 \leq l_{i,j} \leq r_{i,j} \leq 9$
### 说明
- $B_1, B_2, B_3$ 是在约束范围内随机生成的。
- 每个格子的 $l_{i,j}, r_{i,j}$ 是在 $1$ 到 $9$ 之间独立随机生成的。如果 $l_{i,j}$ 大于 $r_{i,j}$,会交换这两个值的位置。
### 示例及其他
[可下载示例输入(Example01~03)和输入验证程序(C++)的链接在这里。](https://img.atcoder.jp/chokudai004/cca3bf4eb85d43be4112d70c0e7f275b.zip)
**本翻译由 AI 自动生成**