AT_chokudai005_a カラフルパネル

有一个 $N \times N$ 的面板，由 $K$ 种不同颜色的方格组成。你的任务是通过触摸面板，使得尽可能多的面板变为同一种颜色。 初始时，每个面板是由颜色 $1$ 到颜色 $K$ 中的一种随机颜色涂成。你可以选择一个面板，通过触摸来将其更改为你期望的颜色。当你选择一个颜色为 $i$ 的面板，并更改其为颜色 $j$ 时，与其相连的、颜色是 $i$ 的面板也会同时更改为颜色 $j$。 游戏的得分规则如下： - 最多的单一颜色所覆盖的面板数乘以 $100$ 即为你的得分。 - 每触摸一次面板，扣除 $1$ 分。 - 如果触摸次数超过 $10000$，系统会崩溃，最终得分为 $0$。 给定初始面板状态，请编写出一种最优的触摸方案，争取获得最高得分。 注意：所有的输入数据是公开的，每组数据有一个唯一的编号 id。可以利用这些数据来解题。此外，我们提供了 [C++ 实现的输入输出验证工具](https://img.atcoder.jp/chokudai005/chekcer.zip)，可用于检查你的解法。

输入包括以下信息： > $id$ $N$ $K$ $S_1$ $S_2$ : $S_N$ 其中： - $id$ 是测试用例的编号。 - $N$ 是面板的规模。 - $K$ 是颜色的数量。 - $S_i$ 是表示面板的字符串，其中长度为 $N$。第 $i$ 行的面板颜色由此指定。

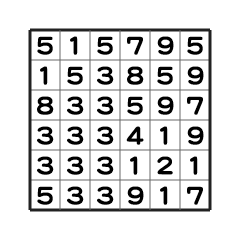
按照下面格式输出： > $Q$ $Y_1$ $X_1$ $C_1$ $Y_2$ $X_2$ $C_2$ : $Y_Q$ $X_Q$ $C_Q$ 其中： - $Q$ 是触摸次数。 - $Y_i, X_i, C_i$ 分别表示第 $i$ 次触摸的行坐标，列坐标及变更后的颜色。 50 个测试用例的总得分是你提交的最终得分。 ## 数据范围 - $1 \leq id \leq 50$ - $N = 100$ - $K = 9$ - $S_i$ 是包含 `1` 到 `K` 之间数字的字符串，表示相应位置的面板颜色。字符串中的每个字符独立随机分配。 - 输入数据可以通过[这个链接中的 zip 文件](https://atcoder.jp/img/chokudai005/dataset.zip)获取。 ### 示例解释 下面的例子使用了一个小规模的输入，仅供解释用途。初始状态下面板如下：  根据输出，我们进行了两次触摸操作。首选触摸的是 $(5,5)$，将其颜色变为 $1$，因为周围没有相邻的色值为 $2$ 的面板，所以只有这个面板的颜色被更改。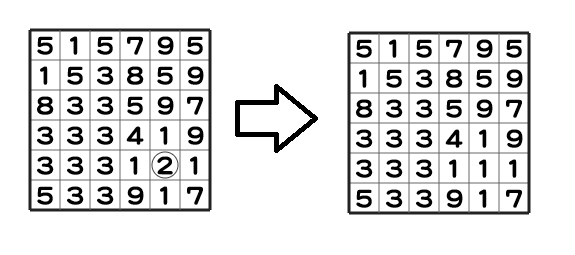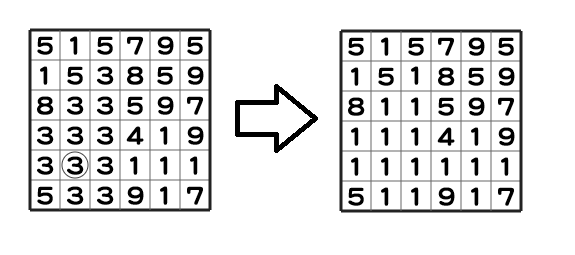  然后触摸 $(5,2)$，将其颜色变为 $1$，这样一来方格色 $3$ 的面板及与其相连的周围面板也一并变为了色 $1$：  完成所有操作后，最多的颜色是 $1$，一共有 $18$ 个面板。最终得分为 $18 \times 100 - 2 = 1798$ 分。 **本翻译由 AI 自动生成**

### 制約 - $ 1 $ ≦ id ≦ $ 50 $ - $ N $ = $ 100 $ - $ K $ = $ 9 $ - $ S_i $ は $ N $ 文字の文字列であり、 $ j $ 番目の文字 $ S_{i,j} $ は、`1`~`K` の $ K $ 種類である。これは、上から $ i $ 番目、左から $ j $ 番目(以下$ (i,j) $と表す）のパネルが$ S_{i,j} $ 色であることを表す。 - $ S $ に使われる文字は、`1`~`K`まで、均等な確率で独立にランダムで選ばれる。 - 入力は[このリンクから得られるzipファイル](https://atcoder.jp/img/chokudai005/dataset.zip)と同一のものが与えられる。 ### Sample Explanation 1 この入力は、説明のため、実際には存在しない小さい入力を使用しております。 パネルは、初期状態では以下のようになっています。 !\[初期状態\](https://atcoder.jp/img/chokudai005/pic1.png) ここから出力の通りに $ 2 $ 回タッチします。 最初は、$ (5,5) $ のパネルを色 $ 1 $ に変えます。この時、隣接するパネルの中で、元のパネルの色である、色 $ 2 $ のものは存在しないため、このパネルのみの色が変わります。 !\[状態1\](https://atcoder.jp/img/chokudai005/pic2.png) 次に、$ (5,2) $ のパネルの色を $ 1 $ に変えます。この時、上下左右に隣接した色 $ 3 $ のパネルを辿って到達できる全てのパネルは、色 $ 1 $ に変化するため、以下のようにパネルが変化します。 !\[状態2\](https://atcoder.jp/img/chokudai005/pic3.png) 全てのパネルを操作した後、最も多い色のパネルは色 $ 1 $ であり、この枚数は $ 18 $ 枚です。 よって、$ 18\ ×\ 100\ -\ 2\ =\ 1798 $ 点が、この解の答えになります。