AT_code_festival_2015_okinawa_j Jungle

[problemUrl]: https://atcoder.jp/contests/code-festival-2015-okinawa-open/tasks/code_festival_2015_okinawa_j

Inputs will be given by standard input in following format. > $ N $ $ M $ $ K $ $ t_1 $ $ t_2 $ : $ t_N $ - At the first line, integer $ N(1≦N≦100,000) $, $ M(1≦M≦N) $, $ K(1≦K≦N) $ will be given. - From the second line there are $ N $ additional lines to give information about sizes of trees. At the $ i_{th} $ line, integer $ t_i(1≦t_i≦1,000,000,000) $ will be given.

Please print the minimum value of the maximum value of the sum of sizes of consecutive $ K $ trees, when we made the optimal cutting choice for the trees in a line. Print a newline at the end of output.

### Problem Wolf Sothe owns a long land in the jungle. In this linear land, $ N $ trees grow at regular intervals. The size of the $ i_{th} $ tree from one end is given as $ t_i $. Inside the jungle it is dark because trees obstruct sunlight. In order to let sunlight shine into the jungle, Wolf Sothe considers cutting some of the $ N $ trees (or cutting no one). More specifically, trees will be cut with the following rules. - Up to $ M $ trees can be cut (no more than $ M $). - Considering the impact on the surrounding ecosystem, it is not allowed to cut two or more trees in arbitrary $ K $ consecutive trees. More precisely, there is not $ i(1≦i≦N-K+1) $ such that $ 2 $ or more trees are cut in the $ i_{th} $, $ (i\ +\ 1)_{th} $, ......, $ (i\ +\ K-1)_{th} $ trees from one end. - If Wolf Sothe cuts the $ i_{th} $ tree from one end, the size of the tree $ t_i $ becomes $ 0 $. - We want the maximum value of the sum of sizes of $ K $ consecutive trees to be as small as possible. Namely, we want to minimize 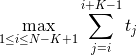 . Since the size of the $ N $ trees and $ M $, $ K $ have been given, when we make the optimal cutting choice for the trees, please obtain the minimum value of the maximum value of the sum of sizes of consecutive $ K $ trees. ### Sample Explanation 1 If Wolf Sothe cuts the $ 3_{rd} $ and $ 6_{th} $ tree, the minimum value of the maximum value of the sum of sizes of consecutive $ 3 $ consecutive trees will be obtained when it is for the $ 2_{nd} $, $ 3_{rd} $, $ 4_{th} $ tree. The sum of sizes is $ 5+0+2=7 $.