AT_code_festival_2015_okinawa_j Jungle

Wolf Sothe 在丛林中拥有一块狭长的土地，上面均匀地生长着 $N$ 棵树。从一边数起，第 $i$ 棵树的大小为 $t_i$。 由于树木阻挡了阳光，使得丛林内光线不足。为了让阳光能够穿透进来，Wolf Sothe 考虑砍掉部分树木（也可以选择一棵不砍）。具体砍树需要遵循以下规则： - 最多可以砍掉 $M$ 棵树。 - 为了不破坏生态系统，在任意连续的 $K$ 棵树中，最多只能砍 1 棵。换句话说，在任何连续 $K$ 棵树里，不能有 2 棵或以上被砍。 - 如果砍掉了第 $i$ 棵树，这棵树的大小就会变为 $0$。 - 我们的目标是使任意连续 $K$ 棵树的大小和的最大值尽量小。也就是，最小化所有连续 $K$ 棵树的大小和的最大值。 根据给定的 $N$ 棵树的大小以及 $M$ 和 $K$ 的值，请在最优砍树方式下，计算出连续 $K$ 棵树的大小和的最大值的最小可能值。

输入通过标准输入给出，格式如下： > $N$ $M$ $K$ > $t_1$ > $t_2$ > ... > $t_N$ - 第一行有三个整数，分别是 $N(1 \le N \le 100,000)$、$M(1 \le M \le N)$ 和 $K(1 \le K \le N)$。 - 接下来的 $N$ 行，每行一个整数 $t_i(1 \le t_i \le 1,000,000,000)$，表示第 $i$ 棵树的大小。

输出在最优砍树操作下，连续 $K$ 棵树的大小和的最大值的最小可能值。输出后需换行。 ## 示例解释 例如，如果 Wolf Sothe 选择砍掉第 3 棵和第 6 棵树，那么在第 2 棵、第 3 棵和第 4 棵树中，连续 3 棵树的大小和最大值将取得 $5 + 0 + 2 = 7$。 **本翻译由 AI 自动生成**

### Problem Wolf Sothe owns a long land in the jungle. In this linear land, $ N $ trees grow at regular intervals. The size of the $ i_{th} $ tree from one end is given as $ t_i $. Inside the jungle it is dark because trees obstruct sunlight. In order to let sunlight shine into the jungle, Wolf Sothe considers cutting some of the $ N $ trees (or cutting no one). More specifically, trees will be cut with the following rules. - Up to $ M $ trees can be cut (no more than $ M $). - Considering the impact on the surrounding ecosystem, it is not allowed to cut two or more trees in arbitrary $ K $ consecutive trees. More precisely, there is not $ i(1≦i≦N-K+1) $ such that $ 2 $ or more trees are cut in the $ i_{th} $, $ (i\ +\ 1)_{th} $, ......, $ (i\ +\ K-1)_{th} $ trees from one end. - If Wolf Sothe cuts the $ i_{th} $ tree from one end, the size of the tree $ t_i $ becomes $ 0 $. - We want the maximum value of the sum of sizes of $ K $ consecutive trees to be as small as possible. Namely, we want to minimize 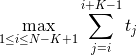 . Since the size of the $ N $ trees and $ M $, $ K $ have been given, when we make the optimal cutting choice for the trees, please obtain the minimum value of the maximum value of the sum of sizes of consecutive $ K $ trees. ### Sample Explanation 1 If Wolf Sothe cuts the $ 3_{rd} $ and $ 6_{th} $ tree, the minimum value of the maximum value of the sum of sizes of consecutive $ 3 $ consecutive trees will be obtained when it is for the $ 2_{nd} $, $ 3_{rd} $, $ 4_{th} $ tree. The sum of sizes is $ 5+0+2=7 $.