AT_code_festival_final_g 魔方陣
题目描述
高桥君非常喜欢魔方阵。
所谓的魔方阵,是指在 $3 \times 3$ 的方格中填入不同的正整数,使得每行、每列和对角线上的三个数的和都相等。
高桥君突然想到,不是求和而是求乘积是否也能构成一种“乘积版魔方阵”。
经过努力的探索,他终于构建出了如下图所示的乘积版本魔方阵。
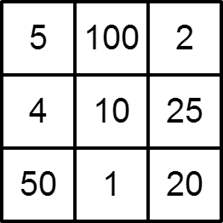
图中所有行、列和对角线的乘积都是 $1000$。
现在,高桥君想知道,中间格子是 $N$ 的乘积版本魔方阵有多少种。
这里,可以通过 $90$ 度旋转或左右反转得到的两个魔方阵不做区分。
请帮助高桥君计算出中间格子是N的乘积版本魔方阵的种类数。
输入格式
输入由以下格式给出:
> $ N $
- 第一行输入乘积版本魔方阵中间值的数字 $ N\ (1\ \leq\ N\ \leq\ 10^{12}) $。
输出格式
输出一个数字,表示中间格子是 $N$ 的乘积版魔方阵的种类数。输出的末尾需要加上换行符。
说明/提示
### Sample Explanation 1
以下の様なパターンは配置されている整数が重複しているので魔方陣ではありません。 !\[\](http://code-festival-2014-final.contest.atcoder.jp/img/other/code\_festival\_2014/G\_same.png) 以下の様なパターンは全て回転や反転によって同じものに変換することができます。 !\[\](http://code-festival-2014-final.contest.atcoder.jp/img/other/code\_festival\_2014/G\_rotate.png)