AT_codefestival_2015_qualB_d マスと駒と色塗り

有 $10^{100}$ 个白色格子横向排列成一行。从左到右，第 $i$ 个格子称为格子 $i$。 此外，有 $N$ 个棋子，第 $i$ 个棋子称为棋子 $i$。 还有一个计数器，可以计数从 $0$ 到 $10^{100}$ 的数。 针对这些格子和棋子，要进行 $N$ 次操作。第 $i$ 次操作（$1 \leq i \leq N$）如下进行： 1. 首先，将棋子 $i$ 放在格子 $S_i$ 上，并将计数器初始化为 $0$。 2. 如果棋子所在的格子是白色，则将该格子涂黑，并将计数器加 $1$；如果棋子所在的格子是黑色，则将棋子移动到右边相邻的格子。 3. 重复步骤 $2$，直到计数器的值变为 $C_i$，此时操作结束。 请你求出所有操作结束后，每个棋子所在的格子的编号。

输入通过标准输入给出，格式如下： > $N$ > $S_1$ $C_1$ > $S_2$ $C_2$ > $\vdots$ > $S_N$ $C_N$ - 第 $1$ 行给出整数 $N$，满足 $1 \leq N \leq 10^5$。 - 接下来的 $N$ 行，每行给出两个整数 $S_i$（$1 \leq S_i \leq 10^9$）、$C_i$（$1 \leq C_i \leq 10^9$），表示第 $i$ 次操作开始时将棋子 $i$ 放在格子 $S_i$，并在计数器达到 $C_i$ 时结束操作。

输出共 $N$ 行。第 $i$ 行输出所有操作结束后棋子 $i$ 所在格子的编号。输出末尾需换行。

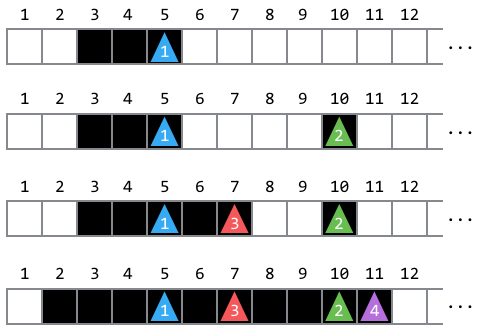
## 部分分 本题设置了部分分。 - 若能正确解决所有操作结束后棋子所在格子的编号均不超过 $10^5$ 的数据集，则可获得 $35$ 分。 - 若能正确解决 $N \leq 1000$ 的数据集，则可额外获得 $40$ 分。 - 若能正确解决无额外限制的数据集，则可额外获得 $25$ 分。 ## 样例解释 1 下图展示了每次操作后的格子和棋子的状态。  ## 样例解释 3 请注意，输出结果可能无法用 $32$ 位整数类型表示。 由 ChatGPT 4.1 翻译