AT_codefestival_2016_final_h Tokaido

有 $N$ 个格子排成一行，从左到右依次编号为 $1$ 到 $N$。すぬけくん和りんごさん打算用这些格子玩如下的棋盘游戏。 1. 首先，すぬけくん会在每个格子上写一个整数。 2. 两位玩家各自准备一个棋子，すぬけくん将自己的棋子放在第 $1$ 个格子，りんごさん将自己的棋子放在第 $2$ 个格子。 3. 棋子在对方棋子左侧的玩家可以移动自己的棋子。棋子的移动目标必须是当前所在格子右侧、且没有对方棋子的格子。 4. 重复第 3 步，直到没有棋子可以再移动为止，游戏结束。 5. 游戏结束时，每位玩家的得分为其棋子曾经停留过的所有格子上所写整数的总和。 すぬけくん已经在第 $i$ 个格子（$1 \leq i \leq N-1$）上写好了整数 $A_i$，但还没有在第 $N$ 个格子上写整数。现在，すぬけくん有 $M$ 个整数 $X_1, X_2, ..., X_M$，他想分别将这些数写在第 $N$ 个格子上，并计算每种情况下“（すぬけくん的得分）−（りんごさん的得分）”的值。 注意，每位玩家都会采取使“（自己的得分）−（对方的得分）”最大化的走法。

输入通过标准输入给出，格式如下： > $N\ A_1\ A_2\ ...\ A_{N-1}\ M\ X_1\ X_2\ ...\ X_M$

对于每个 $X_1, ..., X_M$，分别输出将该数写在第 $N$ 个格子时“（すぬけくん的得分）−（りんごさん的得分）”的值，每行输出一个结果。

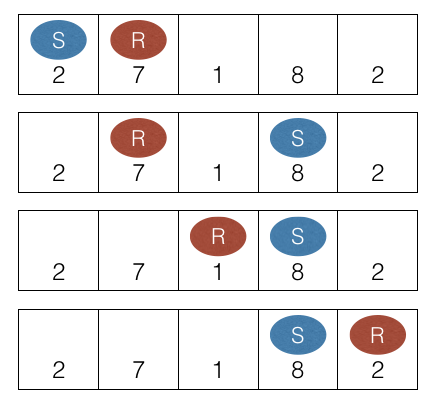
### 限制条件 - $3 \leq N \leq 200,\!000$ - $0 \leq A_i \leq 10^6$ - 所有 $A_i$ 的总和不超过 $10^6$ - $1 \leq M \leq 200,\!000$ - $0 \leq X_i \leq 10^9$ ### 部分得分 - 如果能正确解决 $M=1$ 的数据集，将获得 $700$ 分。 - 如果能正确解决没有额外限制的数据集，将额外获得 $900$ 分。 ### 样例说明 1 游戏的进行如下图所示。S 表示すぬけくん的棋子，R 表示りんごさん的棋子。  两位玩家的得分都是 $10$，因此“（すぬけくん的得分）−（りんごさん的得分）”为 $0$。 由 ChatGPT 4.1 翻译