AT_codefestival_2016_final_j Neue Spiel
题目描述
有一个 $n$ 行,$n$ 列的正方形,共 $n\times n$ 个空格。
可以从上下左右四个方向推入方块,共 $ 4\times n$ 个插入口,编号为:
- 上侧从左到右:$U_1,U_2,\cdots,U_n $
- 下侧从左到右:$D_1,D_2,\cdots,D_n $
- 左侧从上到下:$L_1,L_2,\cdots,L_n $
- 右侧从上到下:$R_1,R_2,\cdots,R_n $

如图是插入口的编号,方块可以推动其他方块,使其往推入方向移动一格,但不能把方块推出正方形外。
你有 $n\times n$ 个方块,全部都要推入正方形内。每个插入口的推入次数有一定的限制,方向 $U_i$ 只能推入 $U_i$ 次,$D_i$ 只能推入 $D_i$ 次,$L_i$ 只能推入 $L_i$ 次,$R_i$ 只能推入 $R_i$ 次。
你需要判断这样推入是否可行,如果可行请输出一种方案
输入格式
第一行一个整数 $n$ 表示正方形边长,接下来第二至第五行分别表示 $ U_i,D_i,L_i,R_i$。
输出格式
如果可以插入 $ n\times n $ 个方块,使得每一格都放置 $1$ 个方块,那么按照应该插入口的号码的顺序,每一行输出一个插入口号码。 不可能的情况下,请输出 `NO` 代替。 另外,在考虑多个插入顺序的情况下,输出其中的 1 个即可。
说明/提示
### 数据范围
- $ 1\leq n \leq 300 $
- $ U_i,D_i,L_i,R_i $ 都是自然数。
- $ U_i,D_i,L_i,R_i $ 的和与 $n \times n$ 相等。
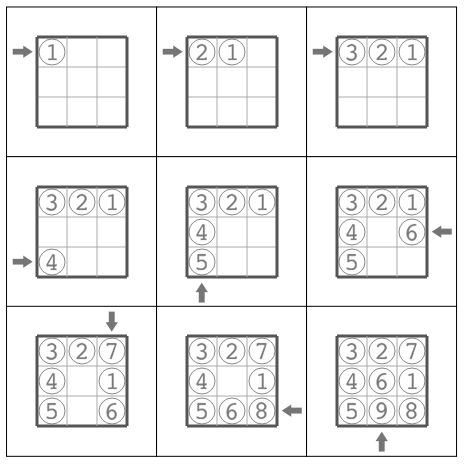
## Sample Explanation 1
样例解释:如下图