AT_codequeen2023_final_b N-Queens Problem

縦に $ N $ マス、横に $ N $ マスからなる、マス目状に区切られた盤面があります。上から $ i $ 番目 $ (1 \leq i \leq N) $ 、左から $ j $ 番目 $ (1 \leq j \leq N) $ のマスを、マス $ (i, j) $ と呼ぶことにします。 盤面には $ N-1 $ 個のクイーンが配置されており、 $ i $ 番目のクイーンはマス $ (r_i, c_i) $ にあります。 ここで、盤面が次の条件を満たすとき、盤面は ***良い状態*** です。 - 盤面上のどの縦・横・斜め 45 度のマス目の列を見ても、クイーンが $ 2 $ つ以上存在しない。 また、与えられる盤面は *良い状態* であることが保証されます。 この盤面に対して、*良い状態* を保ちつつクイーンを追加で $ 1 $ 個配置することができるかを判定し、できる場合は配置する位置を出力してください。

入力は以下の形式で標準入力から与えられます。 > $ N $ $ r_1 $ $ c_1 $ $ r_2 $ $ c_2 $ $ \vdots $ $ r_{N-1} $ $ c_{N-1} $

マス $ (i, j) $ にクイーンを配置できる場合、次の形式で出力してください。答えが複数存在する場合、どれを出力しても正解となります。 > $ i $ $ j $ どこにも配置できない場合は `-1` を出力してください。

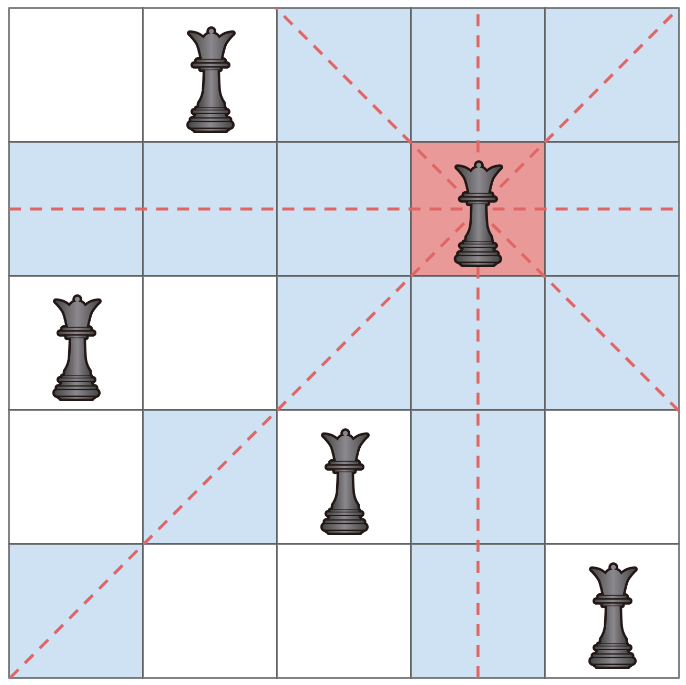
### Sample Explanation 1 マス $ (2, 4) $ を通る、どの縦・横・斜め 45 度のマス目の列を見ても、クイーンは置かれていません。よって、 $ (2, 4) $ にクイーンを置いた後も *良い状態* が保たれます。  ### Constraints - 入力はすべて整数で与えられる - $ 2 \leq N \leq 5{,}000 $ - $ 1 \leq r_i, c_i \leq N $ $ (1 \leq i \leq N - 1) $ - 与えられる盤面は *良い状態* である