AT_codequeen2023_final_f Queen's Crown

在满足以下条件的情况下，在二维平面上放置 $N$ 个点 $P_1, P_2, \ldots, P_N$。在这些条件下，求 $N$ 边形 $P_1P_2\dots P_N$ 的最大面积。设从原点到点 $P_i$ 的连线与 $x$ 轴正方向的夹角为 $\theta_i\ \mathrm{rad}$。 - 第 $i$ 个点 $P_i$ 位于以原点为中心、半径为 $R_i$ 的圆周上。 - 给定的 $R$ 满足 $R_1 = R_N$ 且 $R_1, R_N \leq R_i\ (1 \leq i \leq N)$。 - $\displaystyle \frac{\pi}{2N} \leq \theta_{i+1} -\theta_{i}\ (1 \leq i \leq N-1)$（14:07 修正） - $\theta_1 = 0$, $\theta_N = \frac{2\pi}{3}$ $\displaystyle x\ \mathrm{rad}$ 的定义为：半径为 $1$，弧长为 $x$ 的扇形的圆心角定义为 $x\ \mathrm{rad}$。$x\ \mathrm{rad}$ 相当于 $\frac{180}{\pi} x$ 度。

输入按以下格式从标准输入读入。 > $ N $ $ R_1 $ $ R_2 $ $ \ldots $ $ R_N $

请输出答案。如果你的输出与真值的绝对误差或相对误差不超过 $10^{-6}$，则将被判定为正确。

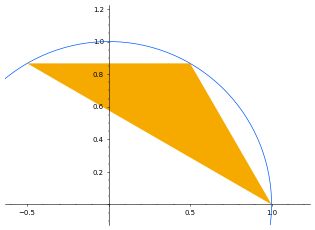
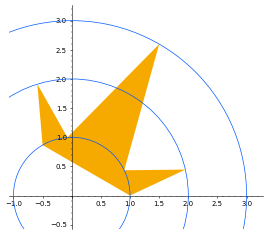
### 样例解释 1 若将 $3$ 个点 $P_1, P_2, P_3$ 分别设为 $ (1,0),\ (\frac{1}{2},\frac{\sqrt{3}}{2}),\ (-\frac{1}{2},\frac{\sqrt{3}}{2}) $，则三角形 $P_1P_2P_3$ 的面积为 $\frac{\sqrt{3}}{4}$，这在所有限制条件内已达最大。  ### 样例解释 2 若将 $7$ 个点 $P_1, P_2, \ldots, P_7$ 恰当设置，则七边形 $P_1P_2\dots P_7$ 的面积约为 $2.147031208123904$，这在所有限制条件内已达最大。  ### 数据范围 - 输入均为整数 - $3 \leq N \leq 100{,}000$ - $0 < R_i \leq 1{,}000\ (1 \leq i \leq N)$ - $R_1 = R_N$ 且 $R_1, R_N \leq R_i\ (1 \leq i \leq N)$ 由 ChatGPT 5 翻译