AT_codequeen2023_final_f Queen's Crown

以下の条件を満たす様に二次元平面上に $ N $ 個の点 $ P_1 $ , $ P_2 $ , $ \ldots $ , $ P_N $ を置きます。この条件の元、 $ N $ 角形 $ P_1 P_2 \dots P_N $ の面積の最大値を求めてください。ただし、原点と点 $ P_i $ を結ぶ直線の $ x $ 軸正の向きとのなす角を $ \theta_i\ \mathrm{rad} $ とします。 - $ i $ 番目の点 $ P_i $ は原点を中心とする半径 $ R_i $ の円周上に存在する - 与えられる $ R $ は、 $ \displaystyle R_1 = R_N $ かつ $ \displaystyle R_1, R_N \leq R_i $ $ (1 \leq i \leq N) $ を満たすことが保証されます - $ \displaystyle \frac{\pi}{2N} \leq \theta_{i+1} -\theta_{i} $ $ (1 \leq i \leq N-1) $ (14:07 修正) - $ \displaystyle \theta_1 = 0 $ , $ \displaystyle \theta_N = \frac{2\pi}{3} $ $ \displaystyle x\ \mathrm{rad} $ の定義 半径が $ 1 $ で弧の長さが $ x $ である様な扇形の中心角を $ \displaystyle x\ \mathrm{rad} $ と定義します。 $ \displaystyle x\ \mathrm{rad} $ は $ \displaystyle \frac{180}{\pi} x $ 度と等しい角度となります。

入力は以下の形式で標準入力から与えられます。 > $ N $ $ R_1 $ $ R_2 $ $ \ldots $ $ R_N $

答えを出力してください。なお、真の解との絶対誤差または相対誤差が $ 10^{−6} $ 以下であれば正解として扱われる事が保証されます。

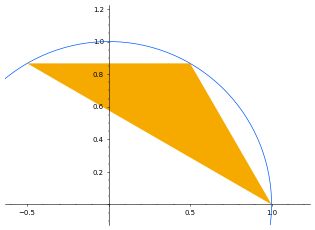
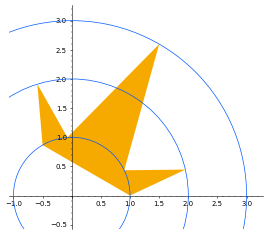
### Sample Explanation 1 $ 3 $ 個の点 $ P_1 $ , $ P_2 $ , $ P_3 $ を ( $ (1,0) $ , $ (\frac{1}{2},\frac{\sqrt{3}}{2}) $ , $ (-\frac{1}{2},\frac{\sqrt{3}}{2}) $ ) と設定すると三角形 $ P_1P_2P_3 $ の面積は $ \frac{\sqrt{3}}{4} $ となり、これは制約内における最大値となります。  ### Sample Explanation 2 $ 7 $ 個の点 $ P_1 $ , $ P_2 $ , $ \ldots $ , $ P_7 $ を適切に設定すると七角形 $ P_1P_2\dots P_7 $ の面積は約 $ 2.147031208123904 $ となり、これは制約内における最大値となります。  ### Constraints - 入力はすべて整数で与えられる - $ 3 \leq N \leq 100{,}000 $ - $ 0< R_i \leq 1{,}000 $ $ (1 \leq i \leq N) $ - $ R_1=R_N $ かつ $ R_1, R_N \leq R_i $ $ (1 \leq i \leq N) $