AT_ddcc2017_final_a 正方形のチップ２

[problemUrl]: https://atcoder.jp/contests/ddcc2017-final/tasks/ddcc2017_final_a 直径 $ 200 $ mmのウェーハ（円盤状の金属の薄い板）と、直径 $ 300 $ mmのウェーハがあります。 この $ 2 $ つのウェーハから、縦横の長さが $ K $ mmの正方形のチップを作成しようとしています。 垂直方向・水平方向の $ 2 $ 方向に、 円の端から $ K $ mmずつ等間隔にウェーハを切断していくことで、正方形のチップを作成していきます。 この時、直径 $ 200 $ mmのウェーハで取れるチップの数と、直径 $ 300 $ mmのウェーハから取れるチップの数を求めてください。 例えば、 $ K=20 $ の時、以下のようにチップを作成することができます。直径 $ 200 $ mmのウェーハからは $ 60 $ 個、直径 $ 300 $ mmのウェーハからは $ 145 $ 個のチップを取ることができます。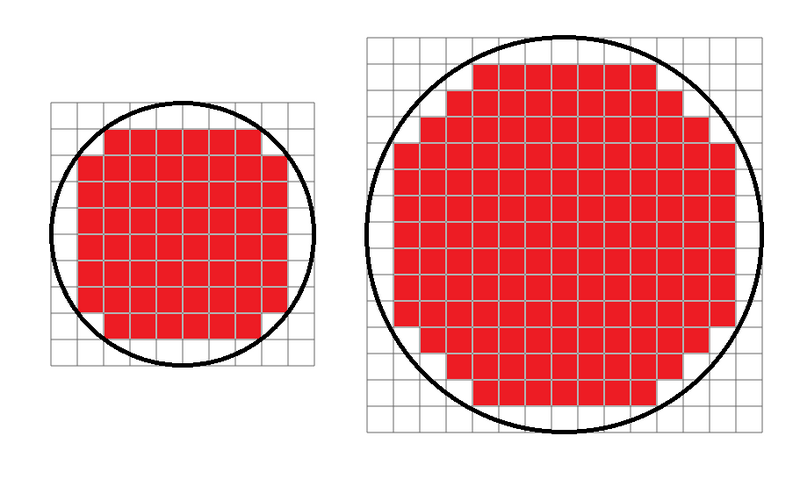 $ K=20 $の時の、ウェーハからチップを取った時の図

入力は以下の形式で標準入力から与えられる。 > $ K $

求めた答えを、直径 $ 200 $ mm、直径 $ 300 $ mm の順にスペース区切りで $ 1 $ 行で出力してください。

### 制約 - $ 4\ ≦\ K\ ≦\ 50 $ - $ K $ は $ 200 $ および $ 300 $ の約数である。つまり、どちらのウェーハについても、円の端から端まで、あまりなしで等間隔に切断することが可能である。 ### Sample Explanation 1 \- 問題文中の例で与えられた入力です。