AT_ddcc2018_qual_c チップ・ストーリー　～白銀編～

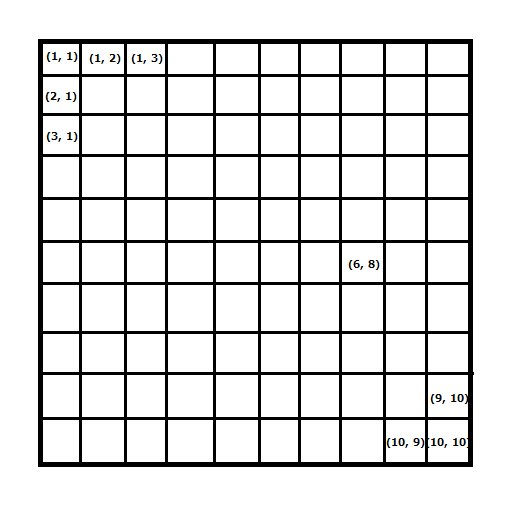
[problemUrl]: https://atcoder.jp/contests/ddcc2019-qual/tasks/ddcc2018_qual_c 高橋君の飼い犬の BISCO は, ディスコ株式会社で働いている. ある日, BISCO は 10 年間の功績を認められ, 社長の WISCO からプレゼントとして正方形のチップを $ 100 $ 枚渡された. BISCO は, これらのチップを以下のように $ 10 $ 行 $ 10 $ 列に並べた.  ここで, 上から $ a $ 番目, 左から $ b $ 番目にあるチップを「チップ $ (a,\ b) $」と表す. さて, BISCO はこれらのチップに以下のようにして整数を書き込むことにした. - まず, 数列 $ P\ =\ (P_1,\ P_2,\ P_3,\ ...,\ P_{10}) $ と $ Q\ =\ (Q_1,\ Q_2,\ Q_3,\ ...,\ Q_{10}) $ を決める. これらの項の値はすべて**正の整数**でなければならない. - 次に, 各チップ $ (i,\ j) $ に整数 $ P_i\ \times\ Q_j $ を書き込む. - このとき, チップに書き込む整数はすべて $ 1 $ 以上 $ N $ 以下でなければならない. この条件が満たされたときのみ, 書き込みが成功する. BISCO は, 書き込みが成功するような数列 $ P,\ Q $ の決め方が何通り存在するかに興味を持った. 彼のために, 書き込みが成功するような $ (P_1,\ P_2,\ P_3,\ ...,\ P_{10},\ Q_1,\ Q_2,\ Q_3,\ ...,\ Q_{10}) $ の組合せとして考えられるものの個数を $ 1\ 000\ 000\ 007 $ で割った余りを求めなさい.

入力は, 以下の形式で標準入力から与えられる. > $ N $

書き込みが成功するような $ (P_1,\ P_2,\ P_3,\ ...,\ P_{10},\ Q_1,\ Q_2,\ Q_3,\ ...,\ Q_{10}) $ の組合せの個数を $ 1\ 000\ 000\ 007 $ で割った余りを出力しなさい.

### 制約 - $ N $ は $ 1 $ 以上 $ 100\ 000 $ 以下の整数 ### Sample Explanation 1 $ N\ =\ 1 $ のとき, 数列 $ P,\ Q $ のすべての項の値を $ 1 $ とするしかない. この場合, すべてのチップに $ 1\ \times\ 1\ =\ 1 $ が書き込まれ, 書き込みは成功する. ### Sample Explanation 4 求めたい組合せの個数を $ 1\ 000\ 000\ 007 $ で割った余りを出力せよ.