AT_ddcc_2016_final_b デュアルカット

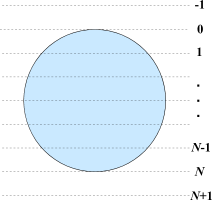
我们有一个半径为 $ R $ 的*晶圆*，需要将其在水平方向上等间隔地切成 $ N $ 份。晶圆是一种用于制造某些部件的薄圆盘。 为了将晶圆等分，我们需要使用 $ N-1 $ 条称为*切割线*的直线。这些切割线依次标号为 $ 1 $ 到 $ N-1 $。另外，为便于讨论，我们假设存在标号为 $ 0 $ 和 $ N $ 的切割线，其长度为 $ 0 $。 示意图如下所示：  我们采用一种称为*双切*的方法进行切割。在每次操作中，我们使用两把刀同时切断两条切割线。然而，由于机器的限制，选中的两条切割线必须保持一定的距离。如果我们选择的两条切割线编号为 $ i $ 和 $ j\ (i < j) $，就必须满足 $ i+M \le j $。在本问题中，允许对同一条切割线多次操作，也允许操作编号为 $ 0 $ 或 $ N $ 的切割线。 当同时操作第 $ i $ 和第 $ j $ 条切割线时，*切割长度*是这两条切割线中较长的一条的长度。第 $ i $ 条切割线的长度是指它与晶圆的交点之间线段的长度，而编号为 $ 0 $ 或 $ N $ 的切割线长度为 $ 0 $。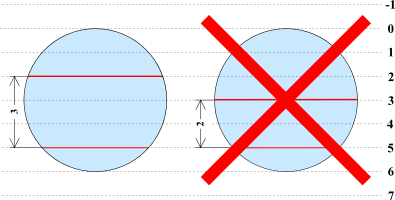 以下是计算机的具体操作示例：如图所示，当 $ N=6, M=3 $，我们选择 $ i=2, j=5 $，则图中的第 2 和第 5 条切割线将被操作。切割长度为第 2 条切割线的长度，因为它比第 5 条长。图中红色线为切割线的长度。注意，右图中的操作 $ i=3, j=5 $ 不被允许，因为它不满足 $ i+M \le j $ 的条件。  为了将晶圆成功切成 $ N $ 份，每一条标号为 $ 1 $ 到 $ N-1 $ 的切割线至少要被操作一次。我们的目标是通过巧妙的操作，使所有切割长度的总和达到最小。请给出这个最小总和。

输入通过标准输入给出： > $ R $ $ N $ $ M $

输出一个数字，表示最小切割长度总和。只要绝对误差或相对误差不超过 $ 10^{-6} $，结果即为正确。

- $ 1 \le R \le 10^3 $ - $ 2 \le N \le 10^3 $ - $ 1 \le M \le N - 1 $ - $ R $ 是整数 ### 部分得分 - 如果能解决 $ M=1 $ 的数据集，可以获得 300 分。 - 能解决没有额外限制的数据集，可额外获得 400 分。 ### 样例解释 1 以下是一个最优操作顺序： - 切割第 1 和第 2 条切割线。 - 切割第 0 和第 3 条切割线。 该操作满足部分得分条件。 ### 样例解释 2 以下是一个最优操作顺序： - 切割第 0 和第 3 条切割线。 - 切割第 1 和第 4 条切割线。 - 切割第 2 和第 5 条切割线。 注意，由于 $ M $ 为 3，因此无法同时切割第 1 和第 2 条切割线，也无法同时切割第 1 和第 3 条切割线，这不符合机器的限制。 **本翻译由 AI 自动生成**