AT_ddcc_2016_final_b デュアルカット

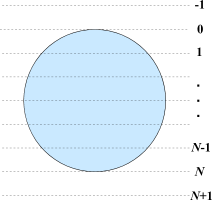
[problemUrl]: https://atcoder.jp/contests/ddcc2016-final/tasks/ddcc_2016_final_b 半径 $ R $ の*ウェーハ*を水平方向に**等間隔**で切って $ N $ 分割することにしました。ウェーハとは、ある部品を作るのに使われる薄い円盤状の物体です。 ウェーハを等間隔で $ N $ 分割するための*カットライン*と呼ばれる線が $ N-1 $ 本あります。 カットラインには上から順に $ 1\ ～\ N-1 $ の番号が付いています。 また、下図に示されるように $ 0 $ 以下や $ N $ 以上の番号のカットラインも便宜上存在することにします。  ウェーハを $ N $ 分割するために*デュアルカット*という手法を用いることにしました。 デュアルカットでは、カットラインに対してカットという操作を何度か行います。 $ 1 $ 回のカットでは、$ 2 $ 枚の刃を使用して $ 2 $ 本のカットラインを同時に切断します。 切断に用いる機械の制約上、$ 2 $ 本のカットラインは一定以上離れている必要があります。 より正確には、同時に切断する $ 2 $ 本のカットラインの番号をそれぞれ $ i,j\ (i\

入力は以下の形式で標準入力から与えられる。 > $ R $ $ N $ $ M $

答えを $ 1 $ 行で出力せよ。絶対誤差、あるいは相対誤差が $ 10^{-6} $ 以下であれば許容される。

### 制約 - $ 1\ ≦\ R\ ≦\ 10^{3} $ - $ 2\ ≦\ N\ ≦\ 10^{3} $ - $ 1\ ≦\ M\ ≦\ N\ -\ 1 $ - $ R $ は整数 ### 部分点 - $ M=1 $ を満たすデータセットに正解した場合は、$ 300 $ 点が与えられる。 - 追加制約のないデータセットに正解した場合は、上記とは別に $ 400 $ 点が与えられる。 ### Sample Explanation 1 以下のようにカットするのが最適な操作の手順の $ 1 $ つです。 - $ 1 $ 番と $ 2 $ 番のカットラインを切断する - $ 0 $ 番と $ 3 $ 番のカットラインを切断する このケースは部分点の制約を満たします。 ### Sample Explanation 2 以下のようにカットするのが最適な操作の手順の $ 1 $ つです。 - $ 0 $ 番と $ 3 $ 番のカットラインを切断する - $ 1 $ 番と $ 4 $ 番のカットラインを切断する - $ 2 $ 番と $ 5 $ 番のカットラインを切断する $ M $ が入力例 $ 1 $ と異なり $ 3 $ であるため、$ 1 $ 番と $ 2 $ 番を同時に切断することや、$ 1 $ 番と $ 3 $ 番を同時に切断することなどは、機械の制約上指定できないことに注意してください。