AT_ddcc_2016_final_e 根付き木とクエリ

给定一棵有 $N$ 个顶点的有根树。每个顶点编号为 $1,\,2,\,\ldots,\,N$，顶点 $1$ 是这棵树的根。第 $i$ 条边（$1 \leq i \leq N-1$）连接顶点 $A_i$ 和顶点 $B_i$，边的长度为 $C_i$，且为无向边。 接下来有 $Q$ 个查询，请按顺序处理。查询有两种类型，输入格式和内容如下： - `1 v k x`：对于以顶点 $v$ 为根的子树，将第 $k$ 代顶点与第 $k+1$ 代顶点之间的每一条边的长度增加 $x$。这里，顶点 $v$ 被定义为第 $1$ 代顶点，直接由第 $n$ 代顶点作为父节点的顶点被定义为第 $n+1$ 代顶点。 - `2 u v`：求顶点 $u$ 到顶点 $v$ 的最短路径长度。 具体请参考样例 $1$。

输入以如下格式从标准输入读入。 > $N$ $A_1$ $B_1$ $C_1$ $:$ $A_{N-1}$ $B_{N-1}$ $C_{N-1}$ $Q$ $Query_1$ $:$ $Query_Q$

对于每个 `2 u v` 格式的查询，按查询给出的顺序，每行输出一个答案。

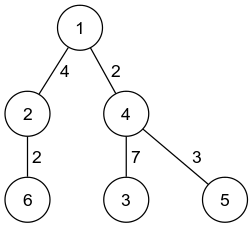
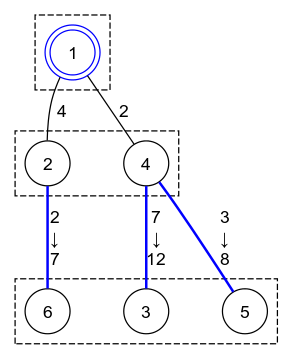
### 约束条件 - $1 \leq N,\, Q \leq 10^{5}$ - $1 \leq A_i,\, B_i \leq N$ - $1 \leq C_i \leq 10^{5}$ - $1 \leq u,\, v,\, k \leq N$ - $1 \leq x \leq 10^5$ - 给定的图是一棵树 - 类型 $2$ 查询中给定的顶点 $u,\, v$ 互不相同 - $C_i,\, x$ 均为整数 ### 样例解释 1 初始时给定如下图的树结构。  处理 `1 1 2 5` 这个查询后，边的长度如下图所示。第 $2$ 代顶点（顶点 $2,\,4$）与第 $3$ 代顶点（顶点 $3,\,5,\,6$）之间的每条边长度都增加了 $5$。  再处理 `1 4 1 2` 这个查询后，边的长度如下图所示。第 $1$ 代顶点（顶点 $4$）与第 $2$ 代顶点（顶点 $3,\,6$）之间的每条边长度都增加了 $2$。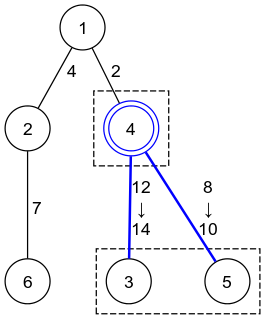  ### 样例解释 2 并非所有加法操作都一定有对应的边存在。 由 ChatGPT 4.1 翻译