AT_ddcc_2016_qual_b ステップカット

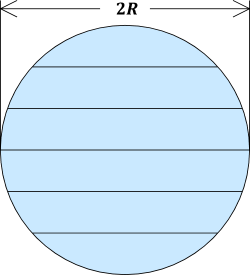
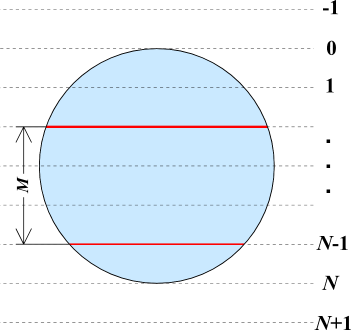
[problemUrl]: https://atcoder.jp/contests/ddcc2016-qual/tasks/ddcc_2016_qual_b 半径 $ R $ のウェーハを、以下の図のように**等間隔**で $ N $ 分割することにしました。この問題におけるウェーハとは、ある部品を作るのに使われる薄い円盤状の物体です。  ウェーハを $ N $ 分割するためのカットラインと呼ばれる線は $ N-1 $ 本あり、上から $ 1,\ \,\ 2,\ \,\ 3,\ \,\ …\ \,\ ,\ \,\ N-1 $ 番のカットラインと呼ぶことにします。また、以下の図に示すような $ -M,\ \,\ …\ \,\ ,\ \,\ -1,\ \,\ 0 $ 番や $ N,\ \,\ N+1,\ \,\ …\ \,\ ,\ \,\ N+M-1 $ 番のカットラインも便宜上存在することにします。  ウェーハを $ N $ 分割するためには $ 1,\ \,\ 2,\ \,\ 3,\ \,\ …\ \,\ ,\ \,\ N-1 $ 番のカットラインに対して機械を使ってそれぞれ $ 2 $ 回ずつカットと呼ばれる処理を行う必要があります。 カットはある機械を使って行われます。 $ 1 $ から $ N+M-1 $ までの番号を指定して機械を稼働させると、$ 2 $ 枚の刃を使ってカットが並列に行われます。 $ i(1≦i≦N+M-1) $ 番を指定して機械を稼働させると $ 1 $ 枚目の刃は $ i $ 番のカットラインのカットを行い、$ 2 $ 枚目の刃は $ i-M $ 番目のカットラインにカットを行います。このときのカット長は長い方のカットラインの長さで表されます。ここで、 $ 0 $ 番や $ N $ 番など $ i(1\ ≦\ i\ ≦\ N-1) $ 番以外のカットラインの長さは $ 0 $ として構いません。 機械の動作の具体例を示します。$ N=6,\ \,\ M=3 $ のときに $ i=5 $ として機械を稼働させると、以下の図のように $ 2 $ 番と $ 5 $ 番のカットラインがカットされます。このときのカット長は $ 2 $ 番のカットラインの方が $ 5 $ 番のカットラインより長いため、$ 2 $ 番のカットラインの長さとなります。  $ 1,\ \,\ 2,\ \,\ 3,\ \,\ …\ \,\ ,\ \,\ N+M-1 $ と順番に指定して機械を稼働させることで、$ 1,\ \,\ 2,\ \,\ 3,\ …\ \,\ ,\ \,\ N\ -1 $ 番のカットラインをそれぞれ $ 2 $ 回カットが行われた状態にすることができます。このような手順でウェーハを $ N $ 分割するときのカット長の総和を出力してください。

入力は以下の形式で標準入力から与えられる。 > $ R $ $ N $ $ M $

答えを $ 1 $ 行で出力せよ。絶対誤差、あるいは相対誤差が $ 10^{-6} $ 以下であれば許容される。

### 制約 - $ 1\ ≦\ R\ ≦\ 10^{5} $ - $ 2\ ≦\ N\ ≦\ 10^{5} $ - $ 1\ ≦\ M\ ≦\ N\ -\ 1 $ - $ R $ は整数 ### Sample Explanation 1 $ 1 $ 枚目の刃が上から $ 1,\ \,\ 2,\ \,\ 3,\ \,\ 4 $ 番のカットラインを順番にカットするとき、それぞれのカット長は $ \sqrt{3},\ \,\ 2,\ \,\ 2,\ \,\ \sqrt{3} $ となります。 $ 0 $ 番のカットラインの長さや、 $ 4 $ 番のカットラインの長さは $ 0 $ として扱ってよいことに注意してください。