AT_donuts_2015_1 ドーナツの体積
题目描述
让我们来计算一个甜甜圈的体积。
将一个平面图形绕某条直线旋转所形成的立体的体积可以通过以下公式计算:
- “平面图形的面积” $ \times $ “平面图形的重心所描绘的圆的周长”
请计算将半径为 $ R $ 的圆绕距离圆心 $ D $ 的直线旋转所形成的甜甜圈形状立体的体积。
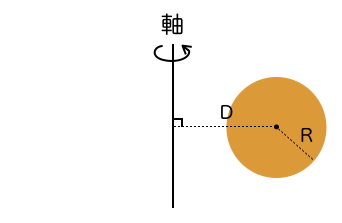
输入格式
输入从标准输入读入,格式如下:
> $ R $ $ D $
- 第 $ 1 $ 行包含两个整数 $ R\ (1\leq R\leq 100),\ D\ (R < D \leq 100)$,以空格分隔。这两个变量与题目描述中的一致。
输出格式
请输出将半径为 $ R $ 的圆绕距离圆心 $ D $ 的直线旋转所形成的立体的体积,输出一行。小数点后可以输出任意位数,但绝对误差不得超过 $ 10^{-2} $。输出末尾需换行。
说明/提示
### 样例解释 1
只需输出将半径为 $ 3 $ 的圆绕距离圆心 $ 5 $ 的直线旋转所形成的立体的体积即可。“平面图形的面积”为 $ 3^2 \times \pi $,“平面图形的重心所描绘的圆的周长”为 $ 5 \times 2 \times \pi $,因此体积为 $ 90 \times \pi^2 $。请注意,圆的重心就是其中心。
由 ChatGPT 4.1 翻译