AT_dwacon2018_final_c XOR ピラミッド

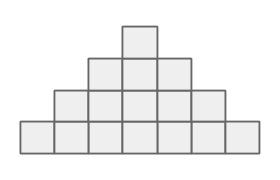
dwango公司的员工尼万戈君正在建造一个 $N$ 层的金字塔。 对于每一层 $1 \leq i \leq N$，从上往下数的第 $i$ 层包含 $2i - 1$ 个横向排列的方块。此外，每层的中间方块纵向排列成了一列。例如，对一个 $4$ 层金字塔而言，它的结构如图所示。  尼万戈君决定使用一个长度为 $2N-1$ 的数列 $a$，将整数填写在金字塔的每个方块中。他首先在第 $N$ 层左边数第 $i$ 个方块中填写整数 $a_i$，然后按照以下规则为其余方块填写整数： - 每个方块中的整数等于它下面三个方块中的整数的异或值，即左下、正下和右下方块中整数的按位异或值。 - 异或运算（$\text{xor}$）表示按位异或操作。 请计算第一层方块中填写的整数。 由于 $N$ 的值可能非常大，数列 $a$ 将通过如下形式提供。具体请参考样例 1。 - 给出整数 $M$ 和两个长度为 $M$ 的数列 $v$ 和 $L$ - 数列 $a$ 由以下形式生成：依次连接数 $v_1$ 重复 $L_1$ 次，$v_2$ 重复 $L_2$ 次，...，$v_M$ 重复 $L_M$ 次。

输入以以下格式提供： > $ M $ $ v_1 $ $ L_1 $ $ : $ $ v_{M} $ $ L_{M} $

输出计算得到的结果。

- $1 \leq M \leq 252,525$ - $0 \leq v_i \leq 10^9$ - $1 \leq L_i \leq 10^9$ - $\sum L_i$ 总是一个不小于3的奇数 - 所有的输入都是整数 ### 样例解释 1 - 数列 $a$ 是由以下序列构成：$(1), (2, 2, 2), (3, 3), (4)$，因此生成的序列为 $(1, 2, 2, 2, 3, 3, 4)$。 - 此时，形成的金字塔如图所示，第一层的方块中填写的是整数 $6$。  ### 样例解释 2 - 如果 $N = 499,999,999$，数列 $a$ 中的内容为 $1$，该数字重复出现 $999,999,999$ 次。此情况下，第一层方块中填写的就是 $1$。 **本翻译由 AI 自动生成**