AT_dwacon2018_final_c XOR ピラミッド

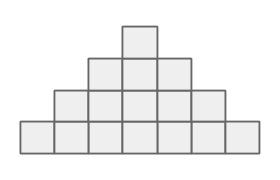
[problemUrl]: https://atcoder.jp/contests/dwacon2018-final/tasks/dwacon2018_final_c dwango社員のニワンゴくんは $ N $ 段のピラミッドを作る仕事をしています。 各 $ 1\ \leq\ i\ \leq\ N $ について、上から $ i $ 段目は $ 2i\ -\ 1 $ 個のブロックが横一列に並んでいます。 また、各段の中央のブロックに着目したとき、これらは縦一列に並んでいます。 例えば $ 4 $ 段のピラミッドの場合、以下の図のようになります。  ニワンゴくんは長さ $ 2N-1 $ の数列 $ a $ を用いて、ピラミッドの各ブロックに整数を書き込むことにしました。 ニワンゴくんは各 $ 1\ \leq\ i\ \leq\ 2N-1 $ について $ N $ 段目の左から $ i $ 番目のブロックに整数 $ a_i $ を書き込んだのち、以下の条件を満たすようにその他のブロックに値を書き込みました。 - 各ブロックに書き込まれる整数は左下、真下、右下のブロックに書き込まれた整数をそれぞれ $ x,\ y,\ z $ として $ x $ $ xor $ $ y $ $ xor $ $ z $ となる - ただし、$ xor $ はビットごとの排他的論理和を表す $ 1 $ 段目のブロックに書き込まれた整数を求めてください。 ただし、$ N $ は非常に大きくなりうるため $ a $ のみが以下の形式で与えられます。詳しくはサンプル $ 1 $ も参照してください。 - 整数 $ M $ と長さ $ M $ の数列 $ v,L $ が与えられる - これは、$ a $ が $ v_1 $ を $ L_{1} $ 回繰り返した数列、$ v_2 $ を $ L_{2} $ 回繰り返した数列、...、$ v_M $ を $ L_{M} $ 回繰り返した数列をこの順で連結して得られる数列であることを表す

入力は以下の形式で標準入力から与えられる。 > $ M $ $ v_1 $ $ L_1 $ $ : $ $ v_{M} $ $ L_{M} $

答えを出力せよ。

### 制約 - $ 1\ \leq\ M\ \leq\ 252{,}525 $ - $ 0\ \leq\ v_i\ \leq\ 10^9 $ - $ 1\ \leq\ L_i\ \leq\ 10^9 $ - $ {\rm\ Σ}{L_i} $ は $ 3 $ 以上の奇数 - 与えられる入力は全て整数 ### Sample Explanation 1 \- $ a $ は $ (1),\ (2,2,2),\ (3,3),\ (4) $ をこの順番で連結した数列である、$ (1,2,2,2,3,3,4) $ となります。 - このとき、以下の図のようなピラミッドが得られ、$ 1 $ 段目のブロックには $ 6 $ が書き込まれます。 !\[ca0b3d434a1e0d28287d47e1ecfbb11d.png\](https://img.atcoder.jp/dwacon2018-final/ca0b3d434a1e0d28287d47e1ecfbb11d.png) ### Sample Explanation 2 \- $ N=499999999 $ で、$ a $ は $ 1 $ が $ 999999999 $ 個繰り返されるような数列です。$ 1 $ 段目のブロックには $ 1 $ が書き込まれます。