AT_dwacon2018_prelims_e ニワンゴくんの家探し

[problemUrl]: https://atcoder.jp/contests/dwacon2018-prelims/tasks/dwacon2018_prelims_e **これはインタラクティブな問題です。** dwango社員のニワンゴくんは $ N $ 頂点の木に住んでいます。 この木の頂点には $ 1 $ から $ N $ までの番号がついています。 この木の $ i $ 番目の辺は頂点 $ a_i $ と頂点 $ b_i $ を双方向につなぐ長さ $ 1 $ の辺です。 ニワンゴくんは **どの頂点の次数も $ 5 $ 以下である** ことを知っています。 この木のいずれかの頂点にニワンゴくんの家がありますが、ニワンゴくんは家がどこにあるかを忘れてしまいました。 ニワンゴくんは自作のプログラムに最大で $ Q $ 回質問を行って、家のある頂点を特定したいです。 プログラムに $ 2 $ つの頂点の番号 $ u,v $ を渡すと、家のある頂点から近い方の頂点の番号が表示されます。 ただし、どちらの頂点も家のある頂点から同じ距離にある場合は `0` が表示されます。 ### Input & Output Format 最初に、標準入力から以下の形式で入力が与えられる： > $ N $ $ Q $ $ a_1 $ $ b_1 $ $ : $ $ a_{N-1} $ $ b_{N-1} $ その後、以下の形式で質問を出力せよ： > ? $ u $ $ v $ ここで、$ u,v $ は $ 1 $ 以上 $ N $ 以下の整数でなくてはならない。 次に、質問の答えが標準入力から以下の形式で与えられる： > $ ans $ ここで、$ ans $ は $ u,v,0 $ のいずれかである。 それぞれの値は以下のことを表す。 - $ u $：$ u $ と $ v $ のうち、家のある頂点に近いのは $ u $ である - $ v $：$ u $ と $ v $ のうち、家のある頂点に近いのは $ v $ である - $ 0 $：$ u $ と $ v $ は、家のある頂点から同じ距離にある 最後に、答えを以下の形式で出力せよ： > ! $ x $ ここで $ x $ は家のある頂点でなくてはならない。

N/A

N/A

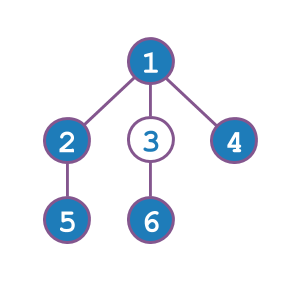
### 制約 - $ 2\ \leq\ N\ \leq\ 2{,}000 $ - $ Q\ =\ 14 $ - $ 1\ \leq\ a_i,b_i\ \leq\ N $ - 与えられるグラフは木 - どの頂点の次数も $ 5 $ 以下 ### 部分点 - どの頂点の次数も $ 2 $ 以下であるようなデータセットに正解した場合、$ 400 $ 点が与えられる。 ### ジャッジ - **出力のあと、標準出力を flush せよ。**従わない場合 `TLE` の可能性がある。 - 答えを出力した後、プログラムをすぐに終了せよ。従わない場合のジャッジの挙動は定義されていない。 - 出力の答えが間違っている場合の挙動は定義されていない( `WA` とは限らない)。 ### 入出力例 これは以下のような木において、頂点 $ 3 $ にニワンゴくんの家がある場合の入出力例です。  Input Output 6 14 1 2 5 2 3 1 3 6 1 4 ? 4 5 4 ? 1 6 0 ? 6 5 6 ! 3- 頂点 $ 4,5 $ のうち、頂点 $ 3 $ に近いのは頂点 $ 4 $ なので $ 4 $ が表示されます。 - 頂点 $ 1,6 $ は頂点 $ 3 $ から同じ距離にあるため、$ 0 $ が表示されます。 - 頂点 $ 6,5 $ のうち、頂点 $ 3 $ に近いのは頂点 $ 6 $ なので $ 6 $ が表示されます。 - 家がある頂点が $ 3 $ だと回答しました。$ 14 $ 回以下の質問で正しい答えを出力したため、正解となります。