AT_dwacon2018_prelims_e ニワンゴくんの家探し
题目描述
**注意:这是一个交互式问题。**
ニワンゴ君是 dwango 公司的员工,他住在一棵有 $N$ 个顶点的树里。树的顶点编号从 $1$ 到 $N$。树中第 $i$ 条边连接了顶点 $a_i$ 和顶点 $b_i$,长度为 $1$。ニワンゴ君知道,树上每个顶点的度数都不超过 $5$。
ニワンゴ君的家位于树上的某个顶点,但他却不记得具体位置了。
为了找到家,ニワンゴ君打算使用自己编写的程序,通过最多 $Q$ 次询问来确认家所在顶点的位置。每次可以向这个程序提供两个顶点编号 $u$ 和 $v$,程序会返回更靠近家所在顶点的编号。若两个顶点距离家同样近,则返回 `0`。
### 输入格式
首次从标准输入获得以下信息:
> $ N $ $ Q $ $ a_1 $ $ b_1 $ $ : $ $ a_{N-1} $ $ b_{N-1} $
之后,每次询问的格式如下:
> ? $ u $ $ v $
其中,$u$ 和 $v$ 是 $1$ 到 $N$ 之间的整数。接下来,根据标准输入获得查询的回答,格式如下:
> $ ans $
这里 $ans$ 是 $u, v, 0$ 之一,含义如下:
- 如果返回 $u$,说明 $u$ 比 $v$ 离家更近。
- 如果返回 $v$,说明 $v$ 比 $u$ 离家更近。
- 如果返回 $0$,说明 $u$ 和 $v$ 离家等距。
最后,请输出家所在顶点的答案,格式为:
> ! $ x $
其中,$x$ 是家所在的正确顶点编号。
输入格式
无
输出格式
无
说明/提示
- $2 \leq N \leq 2{,}000$
- 最大 $Q = 14$
- $1 \leq a_i, b_i \leq N$
- 给定结构是树
- 每个顶点的度数不超过 $5$
### 部分得分
- 若在顶点度数不超过 $2$ 的数据集上正确作答,可获得 $400$ 分。
## 示例说明
以下是一个例子,其中树的结构如图所示,ニワンゴ君的家在顶点 $3$:
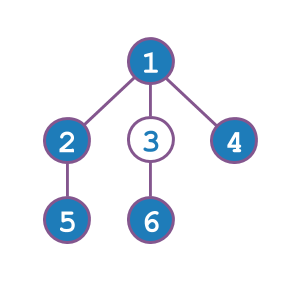
输入:
```
6 14
1 2
5 2
3 1
3 6
1 4
```
输出:
```
? 4 5
4
? 1 6
0
? 6 5
6
! 3
```
- 在顶点 $4$ 和 $5$ 中,顶点 $4$ 更接近家(顶点 $3$),因此返回 $4$。
- 顶点 $1$ 和 $6$ 与家(顶点 $3$)距离相同,因此返回 $0$。
- 在顶点 $6$ 和 $5$ 中,顶点 $6$ 更接近家,因此返回 $6$。
- 最后确认家在顶点 $3$,通过不超过 $14$ 次的询问正确找到了答案,因此为正确解答。
**本翻译由 AI 自动生成**