AT_dwango2015_finals_3 ドライブ
题目描述
ニワンゴ君居住的ニコニコ町有 $N$ 个交叉路口,每个交叉路口编号为 $1$ 到 $N$。此外,有 $M$ 条道路连接着这些交叉路口,每条道路编号为 $1$ 到 $M$。通过第 $i$ 条道路,可以从交叉路口 $A_i$ 到交叉路口 $B_i$,或者从 $B_i$ 到 $A_i$,所需时间为 $2^i$。
ニワンゴ君现在准备出发去兜风。他希望的路线是:从交叉路口 $1$ 出发,经过所有 $M$ 条道路至少一次,并最终回到交叉路口 $1$。请你求出完成这样一次兜风所需的最短时间。由于答案可能非常大,请输出其对 $1,000,000,007$ 取模的结果。
输入格式
输入通过标准输入给出,格式如下:
> $N$ $M$
> $A_1$ $B_1$
> $A_2$ $B_2$
> $\vdots$
> $A_M$ $B_M$
- 第 $1$ 行包含两个整数 $N\ (2\leq N\leq 400,\!000),\ M\ (1\leq M\leq 500,\!000)$,表示ニコニコ町有 $N$ 个交叉路口和 $M$ 条道路。
- 接下来的 $M$ 行,每行包含两个整数 $A_i,\ B_i\ (1\leq A_i\leq N,\ 1\leq B_i\leq N,\ A_i\neq B_i)$,表示第 $i$ 条道路连接交叉路口 $A_i$ 和 $B_i$。不存在两条道路连接同一对交叉路口。保证任意两个交叉路口之间都可以通过若干条道路到达。
输出格式
输出完成兜风所需的最短时间对 $1,000,000,007$ 取模的结果。输出末尾需换行。
说明/提示
## 部分分
本题设有部分分。
- 对于满足 $N\leq 2,\!525$ 且 $M\leq 2,\!525$ 的数据集 $1$,答对可得 $40$ 分。
- 全部测试点均答对,额外可得 $70$ 分。
## 样例解释 1
对于本输入样例,ニコニコ町的结构如下所示。
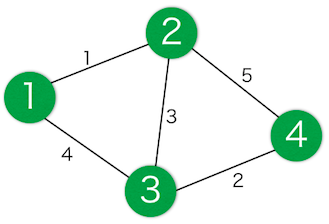
例如,按交叉路口 $1,2,3,4,2,3,1$ 的顺序经过,所需时间为 $2^1 + 2^3 + 2^2 + 2^5 + 2^3 + 2^4 = 70$。
由 ChatGPT 4.1 翻译