AT_dwango2016qual_b 積み鉛筆

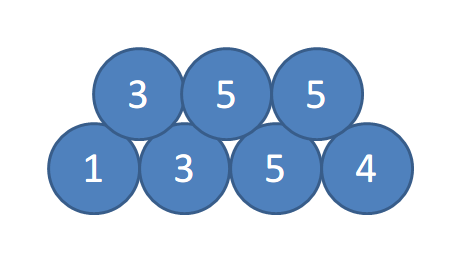[problemUrl]: https://atcoder.jp/contests/dwango2016-prelims/tasks/dwango2016qual_b ニワンゴくんは鉛筆を積むのが好きです。今日は以下の方法で鉛筆を積むことにしました。 まず、$ N $本の鉛筆を左右に$ 1 $列に床に並べます。左から$ i $番目の鉛筆の長さは$ L_i $です。 次に、$ N-1 $本の鉛筆を、床に並べた隣り合う$ 2 $つの鉛筆の間の上に積みます。ただし、上に積む鉛筆の長さは、その下にある$ 2 $つの鉛筆の長さのうち長い方と等しいです。すなわち、上に積む鉛筆のうち、左から$ j $番目のものの長さを$ K_j $と表すと、 $ K_j=max\{L_j,L_{j+1}\} $ が成り立ちます。 例えば、上図のような鉛筆の積み方があります。ここで、円の中に書かれている数は鉛筆の長さを表します。 積んだ鉛筆を上から見たとき、上に積まれた$ N-1 $本の鉛筆の長さのみ見え、$ N $本の土台にある鉛筆の長さは分かりません。この状態で、土台となる$ N $本の鉛筆の長さとしてありうるものを考えるゲームをニワンゴくんは思いつきました。 あなたの仕事はこのゲームに正解するプログラムを書くことです。ただし、土台となる鉛筆の長さの組み合わせは存在することが保証されています。 すなわち、$ N-1 $個の数からなる数列$ \{K_j\} $が与えられたとき、 $ K_j=max\{L_j,L_{j+1}\}\ (1\ ≦\ j\ ≦\ N-1) $がすべての$ j $について成り立つような数列$ \{L_i\} $を求めてください。 ### Input & Output Format 入力は以下の形式で標準入力から与えられる。 > $ N $ $ K_1 $ $ K_2 $ … $ K_{N-1} $ - $ 1 $ 行目には、土台となる鉛筆の本数 $ N\ (2\ ≦\ N\ ≦\ 10^5) $が与えられる。 - $ 2 $ 行目には、上に積まれている鉛筆の長さを表す$ N-1 $個の整数$ K_1,...,K_{N-1} $が空白区切りで与えられる。 - $ 1\ ≦\ K_i\ ≦\ 10^9(1\ ≦\ i\ ≦\ N) $が成り立つ。

N/A

土台となる鉛筆の長さ$ L_1,...,L_N $を空白区切りで1行に出力せよ。出力の末尾には改行をいれること。

### Sample Explanation 1 $ 1,\ 3,\ 5,\ 4 $の長さの鉛筆を土台として$ 3 $本の鉛筆を上に積むと、積まれた鉛筆の長さはそれぞれ$ 3,\ 5,\ 5 $となることが分かります。よって、$ 1,\ 3,\ 5,\ 4 $は答えの条件を満たします。