AT_future_contest_2018_qual_a 山型足し算

[problemUrl]: https://atcoder.jp/contests/future-contest-2018-qual/tasks/future_contest_2018_qual_a $ N $ 行 $ N $ 列のマス目 $ A $ が与えられます。一番左上のマスの位置を $ (0,0) $ と定義します。 このとき、左上のマスから下に $ i\ (0\ ≦\ i\ ≦\ N-1) $ マス、右に $ j\ (0\ ≦\ j\ ≦\ N-1) $ マス進んだマスの位置は $ (j,i) $ で表されます。 また，各マスに整数が書かれており、位置 $ (j,i) $ のマスに書かれている整数を $ A_{i,j} $ で表します。 ここで、マス目に対して全てのマスに書かれている整数が $ 0 $ である状態を「初期マス目」と定義します。 また、マス目 $ P $ に対する「山型足し算」 $ (X,Y,H) $ を以下のように定義します。 - まず，山の中心となるマスの位置 $ (X,Y)\ (0\ ≦\ X,Y\ ≦\ N-1) $ と山の高さを表す整数 $ H\ (1\ ≦\ H\ ≦\ N) $ を指定します。 - その後、全てのマスの $ P_{y,x} $ を $ P_{y,x}\ +\ max(0,\ H\ -\ |x-X|\ -\ |y-Y|) $ に書き換えます。 例として、$ 8 $ 行 $ 8 $ 列の初期マス目であるマス目 $ Q $ を考えます。 マス目 $ Q $ に対して、 $ 3 $ 回の山型足し算 $ (X,Y,H)\ =\ (1,2,5),(5,1,3),(6,6,2) $ を行った後のマス目を以下の図に示します。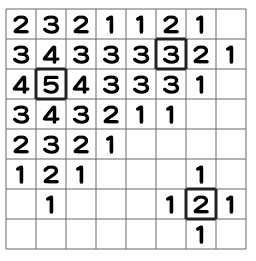 図 山型足し算の例 (空白のマスは $ 0 $ を表す。) 与えられたマス目 $ A $ は、$ N $ 行 $ N $ 列の初期マス目に対して、山型足し算を $ 1000 $ 回行って生成されたマス目です。 あなたの目的は、マス目 $ A $ にできる限り近いマス目を生成する山型足し算の手順を求めることです。 具体的にはまず、$ N $ 行 $ N $ 列の初期マス目であるマス目 $ B $ を用意します。 次に、あなたはマス目 $ B $ に対して山型足し算を最大 $ 1000 $ 回まで行うことができます。 そして、マス目 $ A $ とマス目 $ B $ を比較したとき 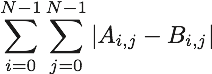 を最小化する山型足し算の手順を求めることを目的とします。 さらに、マス目 $ A $ を生成するような山型足し算の手順が複数存在する場合には、山型足し算の回数を最小化することを目指してください。

入力は以下の形式で与えられる。 > $ A_{0,0} $ $ A_{0,1} $ ... $ A_{0,N-1} $ $ A_{1,0} $ $ A_{1,1} $ ... $ A_{1,N-1} $ : $ A_{N-1,0} $ $ A_{N-1,1} $ ... $ A_{N-1,N-1} $

マス目 $ A $ にできる限り近いマス目 $ B $ を生成する山型足し算の手順を以下の形式で出力せよ。 > $ Q $ $ X_1 $ $ Y_1 $ $ H_1 $ $ X_2 $ $ Y_2 $ $ H_2 $ : $ X_Q $ $ Y_Q $ $ H_Q $ $ 1 $ 行目には山型足し算の回数 $ Q\ (0≦Q≦1000) $ を出力せよ。 $ 1+i\ (1\ ≦\ i\ ≦\ Q) $ 行目には、$ i $ 回目の山型足し算で用いるパラメータ $ (X_i,Y_i,H_i) $ を表す整数をスペース区切りで出力せよ。

### 採点方法 各テストケースの得点は以下のように計算される。 - 縦 $ N $ マス、横 $ N $ マスの初期マス目に対し、あなたのプログラムが出力した山型足し算の手順に従い、マス目 $ B $ を生成する。 - まず、基本点として 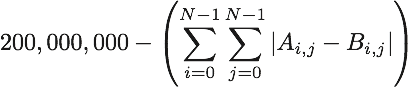 点が得られる。 - マス目 $ A $ とマス目 $ B $ に書かれている整数が全てのマスで一致した場合、山型足し算の回数を $ Q $ とすると、ボーナス点として $ 1,000-Q $ 点が得られる。 問題全体の得点は以下のように計算される。 - テストケースの数は、以下の入力例 $ 1 $ を含む $ 50 $ ケースである。この $ 50 $ ケースの点数の和がプログラムの点数となる。 - 全テストケースのステータスに「AC」以外が存在する場合には、「example\_01」を除く全てのテストケースの点数は0点となるので注意せよ。 ### 制約 - $ N=100 $ - $ 0\ ≦\ A_{i,j}\ ≦\ 100,000 $ - マス目 $ A $ は初期マス目に対して $ 1000 $ 回の山型足し算を行うことで生成されたマス目である。 ### テストケースの生成方法 マス目 $ A $ は初期マス目に対して、$ 1000 $ 回の山型足し算を行うことで生成される。 #### 各回の山型足し算で用いられるパラメータ $ (X,Y,H) $ についての制約 - $ X $ は $ [0,N-1] $ の範囲で、一様乱数によってランダムに選ばれる。 - $ Y $ は $ [0,N-1] $ の範囲で、一様乱数によってランダムに選ばれる。 - $ H $ は $ [1,N] $ の範囲で、一様乱数によってランダムに選ばれる。 ### 入出力例1 [入出力ファイルはこちらから(zip)](https://img.atcoder.jp/future-contest-2018-qual/592b2384afccbe5f23dae7ec7d98b9f3.zip) テストケース「example\_01」が入出力例1に対応します。テストケース「example\_01」も採点対象となります。