AT_future_contest_2018_qual_a 山型足し算

给定一个 $N \times N$ 的矩阵 $A$，其中左上角的格子位置定义为 $(0, 0)$。从这个位置向下移动 $i$ 格（$0 \le i \le N-1$），再向右移动 $j$ 格（$0 \le j \le N-1$）后所到达的格子位置表示为 $(j, i)$。每个格子内包含一个整数，位置 $(j, i)$ 格子的整数用 $A_{i,j}$ 表示。 我们将所有格子内的整数均为 $0$ 的状态视为“初始矩阵”。对于矩阵 $P$，定义“山型加法”$(X, Y, H)$如下： - 首先，指定山的中心位置为 $(X, Y)$，其中 $0 \le X, Y \le N-1$，以及山的高度 $H$，满足 $1 \le H \le N$。 - 然后，将矩阵中所有的格子 $P_{y,x}$ 更新为 $P_{y,x} + \max(0, H - |x-X| - |y-Y|)$。 例如，考虑一个 $8 \times 8$ 的初始矩阵 $Q$。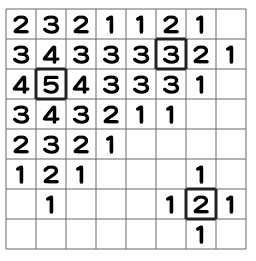对矩阵 $Q$ 依次进行三次山型加法，具体参数为 $(X, Y, H) = (1, 2, 5), (5, 1, 3), (6, 6, 2)$，加法后的结果如图所示：  （图中空白的格子表示数值为 $0$。） 给定矩阵 $A$ 是在初始矩阵上经过最多 1000 次山型加法得到的。你需要设计一种方法，通过山型加法生成一个尽可能接近矩阵 $A$ 的矩阵。 具体操作步骤如下： 1. 准备一个 $N \times N$ 的初始矩阵 $B$。 2. 在矩阵 $B$ 上最多进行 1000 次山型加法。 3. 你的目标是找到一种加法方案，最小化矩阵 $B$ 和矩阵 $A$ 之间的差异。如果存在多种方案能够生成矩阵 $A$，则优先选择操作次数最少的方案。

输入为单行，包含 $N \times N$ 个整数，依次表示矩阵 $A$ 的各个元素： > $A_{0,0} A_{0,1} \ldots A_{0,N-1} A_{1,0} A_{1,1} \ldots A_{N-1,N-1}$

输出为山型加法的步骤，使得生成的矩阵尽可能接近 $A$： 1. 首行输出加法的次数 $Q$，满足 $0 \le Q \le 1000$。 2. 随后 $Q$ 行中，每行输出一次山型加法的参数，以空格分隔：$X_i Y_i H_i$，表示第 $i$ 次山型加法。

### 评分标准 每个测试用例的得分计算方式如下： - 对 $N \times N$ 的初始矩阵应用你的输出的山型加法步骤生成矩阵 $B$。 - 基本分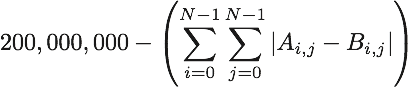：。 - 如果矩阵 $A$ 和 $B$ 的所有格子的整数值都相同，且使用了 $Q$ 次山型加法，则额外获得 $1000 - Q$ 的奖励分。 最终得分为所有测试用例得分之和，共 50 个测试用例，包括输入样例 1。若任何测试用例未通过，则除了“example_01”以外的所有测试用例的得分均为 0。 ### 约束 - $ N = 100 $ - $ 0 \le A_{i,j} \le 100,000 $ - 矩阵 $A$ 是通过初始矩阵执行 1000 次山型加法得到的。 #### 每次山型加法的参数 $(X, Y, H)$ 的约束 - $X$ 和 $Y$ 为区间 $[0, N-1]$ 中的随机整数。 - $H$ 为区间 $[1, N]$ 中的随机整数。 ### 输入输出示例 1 [输入输出文件下载](https://img.atcoder.jp/future-contest-2018-qual/592b2384afccbe5f23dae7ec7d98b9f3.zip) 测试用例“example_01”对应于示例 1，并计入评分。 **本翻译由 AI 自动生成**