AT_gigacode_2019_h 論理回路の構成

有 $N$ 个开关，这些开关编号为 $1, 2, 3, \ldots, N$。每个开关都有两种状态：0 和 1。 你可以使用编号为 $N+1, N+2, \ldots, N+M$ 的 $M$ 个存储单元来构建电路（$M$ 的值可以自由设定）。 这些存储单元支持以下四种操作类型。在接下来的描述中，我们将相关存储单元编号为 $x$。 **① AND 存储单元** 该单元连接两个开关/存储单元，编号为 $u$ 和 $v$，满足 $u < x, v < x$。当且仅当这两个编号 $u$ 和 $v$ 的开关/存储单元的值都为 1 时，编号 $x$ 的存储单元的值为 1，否则为 0。 **② OR 存储单元** 该单元连接两个开关/存储单元，编号为 $u$ 和 $v$，满足 $u < x, v < x$。当至少有一个编号为 $u$ 或 $v$ 的开关/存储单元的值为 1 时，编号 $x$ 的存储单元的值为 1，否则为 0。 **③ XOR 存储单元** 该单元连接两个开关/存储单元，编号为 $u$ 和 $v$，满足 $u < x, v < x$。当且仅当编号 $u$ 和 $v$ 的开关/存储单元的值中有且只有一个为 1 时，编号 $x$ 的存储单元的值为 1，否则为 0。 **④ NOT 存储单元** 该单元连接一个开关/存储单元，编号为 $u$，满足 $u < x$。当编号 $u$ 的开关/存储单元的值为 0 时，编号 $x$ 的存储单元的值为 1，否则为 0。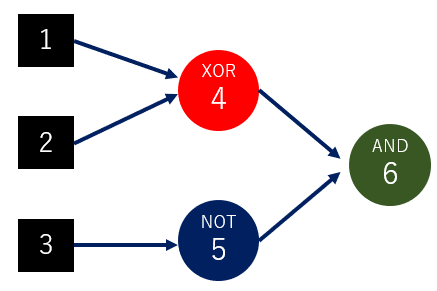 例如，考虑如下电路图：  对于此电路，各种开关状态下的存储单元状态如下： | 开关1 | 开关2 | 开关3 | 内存4 | 内存5 | 内存6 | |------|------|------|------|------|------| | 0 | 0 | 0 | 0 | 1 | 0 | | 0 | 0 | 1 | 0 | 0 | 0 | | 0 | 1 | 0 | 1 | 1 | 1 | | 0 | 1 | 1 | 1 | 0 | 0 | | 1 | 0 | 0 | 0 | 0 | 0 | | 1 | 0 | 1 | 1 | 0 | 0 | | 1 | 1 | 0 | 0 | 1 | 1 | | 1 | 1 | 1 | 0 | 0 | 0 | 因此，只有当开关1, 开关2, 开关3的状态分别为 {0, 1, 0} 或 {1, 0, 0} 时，存储单元6 的值才为 1。 请解决下面两个问题： **当 T = 1 时** 开关的状态有 $2^N$ 种可能。请构建一个电路，使得仅有 $K$ 种状态下，编号为 $N+M$ 的存储单元（若 $M=0$ 则为开关）的值为 1。 请注意，使用的存储单元数量不能超过 $2^{N} \times 4N$。 **当 T = 2 时** 请构建一个电路，使得只有当开关状态为 $S_1, S_2, S_3, \ldots, S_K$ 时，编号为 $N+M$ 的存储单元（若 $M=0$ 则为开关）的值为 1。 请注意，使用的存储单元数量不能超过 50000 个。

输入以以下格式给出： **当 T = 1 时** ``` 1 N K ``` 这里，$N$ 是开关的数量，$K$ 是满足编号为 $N+M$ 的开关（若 $M=0$ 则为存储单元）的值为 1 的状态数。 **当 T = 2 时** ``` 2 N K S_1 S_2 S_3 : S_K ``` 这里，$S_i$ 表示满足编号为 $N+M$ 的开关（若 $M=0$ 则为存储单元）的值为 1 的状态之一。每个 $S_i$ 是一个由 $N$ 个字符组成的字符串，其中第 $i$ 个字符为 `0` 表示第 $i$ 个开关的状态为 0，字符为 `1` 表示状态为 1。例如，若 $N = 4$ 且 $S_i = \text{0101}$，表示开关2和开关4为 1，而开关1和开关3为 0。

请输出构成逻辑电路的方法，格式如下： ``` M (编号为 N+1 的内存信息) (编���为 N+2 的内存信息) (编号为 N+3 的内存信息) : (编号为 N+M 的内存信息) ``` 编号为 $x$ 的内存信息应按以下格式输出： **AND 存储单元的情况** ``` AND u v ``` 表示编号为 $u$ 和 $v$ 的开关/存储单元与编号为 $x$ 的存储单元连接。需满足 $u < x, v < x$（允许 $u = v$）。 **OR 存储单元的情况** ``` OR u v ``` 表示编号为 $u$ 和 $v$ 的开关/存储单元与编号为 $x$ 的存储单元连接。需满足 $u < x, v < x$（允许 $u = v$）。 **XOR 存储单元的情况** ``` XOR u v ``` 表示编号为 $u$ 和 $v$ 的开关/存储单元与编号为 $x$ 的存储单元连接。需满足 $u < x, v < x$（允许 $u = v$）。 **NOT 存储单元的情况** ``` NOT u ``` 表示编号为 $u$ 的开关/存储单元与编号为 $x$ 的存储单元连接。需满足 $u < x$。

### 约束 - $1 \leq T \leq 2$ - $2 \leq N \leq 10$ - $1 \leq K \leq 2^N - 1$ - $T, N, K$ 均为整数 ### 子任务与得分 该题目有两个子任务： 1. (30 分) $T = 1$。 2. (70 分) $T = 2$。 对于子任务 1，每个测试用例的得分如下。该子任务的得分为所有测试用例的最低得分。 - 如果 $2^N \times 4N < M$，得 0 分。 - 如果 $2^N \times 2 < M \leq 2^N \times 4N$，得 10 分。 - 如果 $N^2 < M \leq 2^N \times 2$，得 16 分。 - 如果 $N - 1 < M \leq N^2$，得 23 分。 - 如果 $M \leq N - 1$，得 30 分满分。 对于子任务 2，设所有测试用例中 $M$ 的最大值为 $L_2$，则该子任务的得分为： - 如果 $50,001 \leq L_2$，得 0 分。 - 如果 $4,201 \leq L_2 \leq 50,000$，得 15 分。 - 如果 $3,101 \leq L_2 \leq 4,200$，得 18 分。 - 如果 $2,101 \leq L_2 \leq 3,100$，得 21 分。 - 如果 $1,601 \leq L_2 \leq 2,100$，得 25 分。 - 如果 $1,201 \leq L_2 \leq 1,600$，得 29 分。 - 如果 $751 \leq L_2 \leq 1,200$，得 35 分。 - 如果 $501 \leq L_2 \leq 750$，得 $\lfloor 70 - \frac{L_2 - 500}{8} \rfloor$ 分。 - 如果 $L_2 \leq 500$，得 70 分满分。 ### 样例解释 在给定输出的例子中，当 $N = 2$ 是否满足 $M = 3$，由于 $N$ 介于 $N$ 和 $N^2$ 之间，因此得 23 分。 **本翻译由 AI 自动生成**