AT_hitachi2017_1_a Problem 1

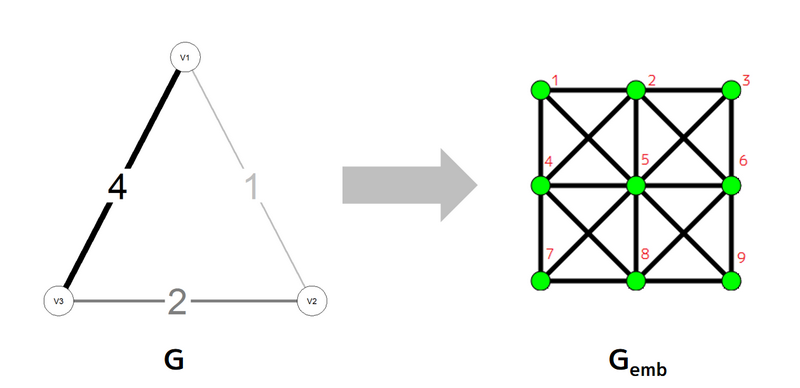
[problemUrl]: https://atcoder.jp/contests/hokudai-hitachi2017-1/tasks/hitachi2017_1_a 頂点集合$ V $、辺集合$ E $からなるグラフを$ G=(V,E) $ とする。二つのグラフ $ G=(V,\ E) $ と $ G_{emb}=(V_{emb},E_{emb}) $ が与えられているとし、グラフ $ G $ の各辺には重みが定義されているとせよ。入力と出力の箇所で説明する制約のもとで、以下で説明する得点ができるだけ高くなるように、 $ V $ のすべての要素に対し $ V_{emb} $ の頂点を対応させよ。なお、 $ G_{emb} $ は以下の図のような、一行に含まれる頂点数と一列に含まれる頂点数が等しい正方形型の [King's Graph](https://en.wikipedia.org/wiki/King%27s_graph) である。King's Graph の頂点の番号付けについては、左上が $ 1 $ であり、以降左から右に順に番号を振り、行末に到達したときは次の行から同様に順に番号を振るものとする。 

入力は以下の形式で標準入力から与えられます。入力はすべて整数値です。 > $ |V| $ $ |E| $ $ u_1 $ $ v_1 $ $ w_1 $ $ u_2 $ $ v_2 $ $ w_2 $ : $ u_{|E|} $ $ v_{|E|} $ $ w_{|E|} $ $ |V_{emb}| $ $ |E_{emb}| $ $ a_1 $ $ b_1 $ $ a_2 $ $ b_2 $ : $ a_{|E_{emb}|} $ $ b_{|E_{emb}|} $ - $ |V| $ と $ |E| $ はグラフ $ G $ の頂点の数と辺の数を表します。 - $ u_i,\ v_i,\ w_i $ はグラフ $ G $ の辺についての情報であり、頂点 $ u_i $ と頂点 $ v_i $ が重み $ w_i $ の辺で接続されていることを表します。 - $ |V_{emb}| $ と $ |E_{emb}| $ はグラフ $ G_{emb} $ の頂点の数と辺の数を表します。 - $ a_i,\ b_i $ はグラフ $ G_{emb} $ の辺についての情報であり、頂点 $ a_i $ と頂点 $ b_i $ が接続されていることを表します。 **グラフ $ G $ についての制約** - $ 2\ \leq\ |V|\ \leq\ 5\ \times\ 10^2 $ - $ 1\ \leq\ |E|\ \leq\ min(|V|(|V|-1)/2,\ 2\ \times\ 10^4) $ - $ 1\ \leq\ u_i\ \lt\ v_i\ \leq\ |V| $ - $ 0\ \leq\ w_i\ \leq\ 15 $ - $ i\ \neq\ j $ ならば、 $ u_i\ \neq\ u_j $ または $ v_i\ \neq\ v_j $ - 与えられるグラフは連結である **グラフ $ G_{emb} $ についての制約** - $ G_{emb} $ は正方形の King's グラフである - $ 4\ \leq\ |V_{emb}|\ \leq\ 3.6\ \times\ 10^3 $ かつ $ |V_{emb}| $ は平方数 - $ |V|\ \leq\ |V_{emb}| $ - $ 1\ \leq\ a_i\ \lt\ b_i\ \leq\ |V_{emb}| $

出力は以下の形式で標準出力に $ |V| $ 行で出力してください。 > $ s_1 $ $ t_1 $ $ s_2 $ $ t_2 $ : $ s_{|V|} $ $ t_{|V|} $ - $ s_i,\ t_i $ は、グラフ $ G $ の頂点 $ s_i $ が、グラフ $ G_{emb} $ の頂点 $ t_i $ と対応していることを表します。 - グラフ $ G $ のすべての頂点に対して対応関係が明らかになっており、かつ $ G $ と対応関係にある $ G_{emb} $ の頂点について、それに対応する $ G $ の頂点は一意に定まらなければいけません。詳しくは、出力についての制約をお読みください。 **出力についての制約** - 出力は $ |V| $ 行からなる - $ 1\ \leq\ s_i\ \leq\ |V| $ - $ 1\ \leq\ t_i\ \leq\ |V_{emb}| $ - $ i\ \neq\ j $ ならば、 $ s_i\ \neq\ s_j $ かつ $ t_i\ \neq\ t_j $

### 得点計算について 各テストケースの得点およびこの問題の得点は、以下のように計算します。 - $ G $ の辺 $ (u,\ v) $ について以下の条件が成り立つときその辺の重みを得点に加算する。条件：$ G_{emb} $ において、$ u $ と対応する $ G_{emb} $ の頂点 $ p $ と、$ v $ と対応する $ G_{emb} $ の頂点 $ q $ の間に辺 $ (p,\ q) $ が存在する。 - テストケースの得点は、$ G $ の辺であって上記の条件を満たす辺の重みの総和です。 - テストケースは全部で $ 30 $ 個（ランダムグラフが18個、完全グラフが12個）あり、各テストケースの得点の合計がこの問題の得点になります。\* - 各テストケースについて、実行制限時間又はメモリを超過する、ないしは出力が正しい出力フォーマットに従っていないものは $ 0 $ 点となります。 \*当初のアナウンスと異なり、最終順位・得点はシステムテストにより決定します。本テストはコンテスト終了後、本テストケースとは異なる、150個のジャッジデータで最終提出をリジャッジすることで評価します。150個のジャッジデータは、テストケースと同じ方法で生成し、90個のランダムグラフ（そのうち40個は各頂点の次数が高々8）と60個の完全グラフで構成します。本テストにより、最終順位が変動するかもしれません。本テストはシード値の特定等、チューニングによる高得点を防ぐためのものであり、AtCoder社様との協議の結果、本テストにて最終順位を決定します。 ### グラフ G の生成について すべてのテストケースについて、与えられるグラフ $ G $ は「ランダムグラフ」または「完全グラフ」のいずれかです。それぞれのグラフの生成方法を以下に簡単に示します。 詳細は[サンプルコード](https://img.atcoder.jp/hokudai-hitachi2017-1/problem1_toolkit_JP_r1.zip)をご覧ください。 **ランダムグラフ** - はじめに、 $ |V| $ 頂点からなる木をランダムに生成し、その後 $ |E|\ -\ |V|\ +\ 1 $ 回ランダムに辺を張り、グラフの各辺についてランダムに重み付けします。 - ランダムグラフのうち $ 8 $ ケースは、各頂点の次数が高々 $ 8 $ であるようなランダムグラフになっています。これは新たに辺を張るときに、すでに頂点の次数が $ 8 $ である頂点を選ばないように生成しています。 **完全グラフ** - $ 1\ \leq\ u\ \lt\ v\ \leq\ |V| $ を満たすすべての $ (u,\ v) $ の組について、重み $ w $ をランダムに設定し辺を張ります。 ### ジェネレータ・テスターおよび参考文献 この問題のジェネレータおよびテスターは[ここ](https://img.atcoder.jp/hokudai-hitachi2017-1/problem1_toolkit_JP_r1.zip)からダウンロードできます。 この問題を解くにあたって、以下の文献が参考になります。こちらを参考にしながら解答を作成しても良いです。 H. Neven, et al., "NIPS 2009 demonstration: Binary classification using hardware implementation of quantum annealing." Quantum (2009): 1-17. ### Sample Explanation 2 この入力例を図示したものは以下の通りです。 !\[\](https://img.atcoder.jp/hokudai-hitachi2017-1/d08f7cdbfde51d8c34ae4da248f15613.png)