AT_hitachi2017_1_a Problem 1

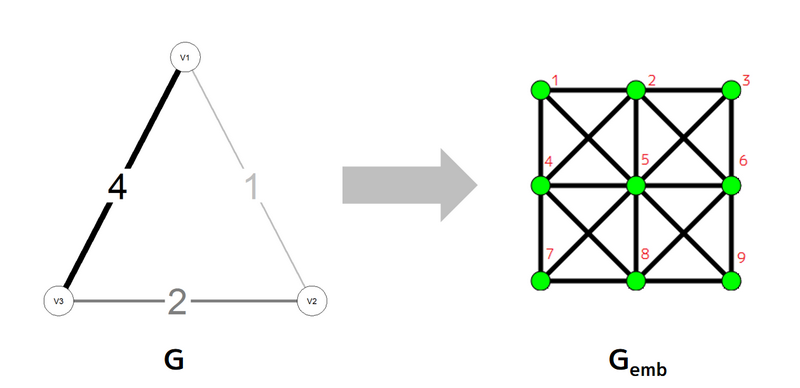
考虑一个由顶点集 $V$ 和边集 $E$ 构成的图 $G=(V, E)$。给定图 $G=(V, E)$ 和 $G_{emb}=(V_{emb}, E_{emb})$，并假设图 $G$ 的每条边都有权重。你的任务是在遵循输入输出约束的前提下，将 $V$ 中的所有顶点与 $V_{emb}$ 的顶点配对，使得得分尽可能高。这其中，$G_{emb}$ 是一个由相等数量行列组成的正方形形状的 King's Graph（“国王图”），顶点编号从左上角的 $1$ 开始，从左到右，然后从上到下依次排列。 

输入通过标准输入提供，格式如下，所有数值均为整数： > $|V|$ $|E|$ $u_1$ $v_1$ $w_1$ $u_2$ $v_2$ $w_2$ : $u_{|E|}$ $v_{|E|}$ $w_{|E|}$ $|V_{emb}|$ $|E_{emb}|$ $a_1$ $b_1$ $a_2$ $b_2$ : $a_{|E_{emb}|}$ $b_{|E_{emb}|}$ - $|V|$ 和 $|E|$ 表示图 $G$ 的顶点数和边数。 - $u_i, v_i, w_i$ 描述图 $G$ 中的边，即顶点 $u_i$ 与顶点 $v_i$ 之间有一条权重为 $w_i$ 的边。 - $|V_{emb}|$ 和 $|E_{emb}|$ 表示图 $G_{emb}$ 的顶点数和边数。 - $a_i, b_i$ 描述图 $G_{emb}$ 中的边，即顶点 $a_i$ 与顶点 $b_i$ 是相连的。

输出应包含 $|V|$ 行，每行格式为： > $s_1$ $t_1$ $s_2$ $t_2$ : $s_{|V|}$ $t_{|V|}$ - $s_i, t_i$ 表示图 $G$ 的顶点 $s_i$ 与图 $G_{emb}$ 的顶点 $t_i$ 对应。 - 所有图 $G$ 的顶点都要有对应且互不冲突的 $G_{emb}$ 中的顶点。具体约束见下文。 ## 数据范围和提示 ### 得分计算 每个测试用例是否得分及得分多少，依据如下条件： - 如果图 $G$ 中的某条边 $(u, v)$，在 $G_{emb}$ 中，$u$ 对应的顶点 $p$ 和 $v$ 对应的顶点 $q$ 之间存在边 $(p, q)$，那么这条边的权重被算入总得分。 - 测试用例的得分是满足上述条件的边之权重总和。 - 一共有 30 个测试用例（分为 18 个随机图和 12 个完全图），所有测试用例得分总和即是问题的最终得分。\* - 如果超出时空限制或输出格式错误，则测试用例得分为 0。 \*与最初宣布不同，最终排名和得分由系统测试决定。系统测试将在比赛结束后用150个不同的判题数据对最终提交进行重新评测，这150个数据中有90个随机图（其中40个图的顶点最大度为8）和60个完全图。这次判题可能导致最终排名变化，目的是防止通过特定种子值调优来获得高分。 ### 图 $G$ 的生成 所有测试用例中的图 $G$ 要么是“随机图”，要么是“完全图”。以下是这两种图的生成方式的简要说明： **随机图** - 首先随机生成一个 $|V|$ 个顶点的树，然后依据需要随机添加 $|E| - |V| + 1$ 条边，其中边的权重也是随机的。 - 在随机图中，有 8 个案例顶点的度数最多为 8，这是通过限制新加边顶点的度数实现的。 **完全图** - 对于所有满足条件 $1 \leq u < v \leq |V|$ 的顶点对 $(u, v)$，随机设置权重 $w$ 并添加边。 ### 生成器、测试器及参考文献 本问题的生成器和测试器可从[此链接](https://img.atcoder.jp/hokudai-hitachi2017-1/problem1_toolkit_JP_r1.zip)下载。 解决该问题时，可参考以下文献： H. Neven, et al., "NIPS 2009 demonstration: Binary classification using hardware implementation of quantum annealing." Quantum (2009): 1-17. ### 示例解释 2 下图展示了输入示例的图形表示：  **本翻译由 AI 自动生成**

### 得点計算について 各テストケースの得点およびこの問題の得点は、以下のように計算します。 - $ G $ の辺 $ (u,\ v) $ について以下の条件が成り立つときその辺の重みを得点に加算する。条件：$ G_{emb} $ において、$ u $ と対応する $ G_{emb} $ の頂点 $ p $ と、$ v $ と対応する $ G_{emb} $ の頂点 $ q $ の間に辺 $ (p,\ q) $ が存在する。 - テストケースの得点は、$ G $ の辺であって上記の条件を満たす辺の重みの総和です。 - テストケースは全部で $ 30 $ 個（ランダムグラフが18個、完全グラフが12個）あり、各テストケースの得点の合計がこの問題の得点になります。\* - 各テストケースについて、実行制限時間又はメモリを超過する、ないしは出力が正しい出力フォーマットに従っていないものは $ 0 $ 点となります。 \*当初のアナウンスと異なり、最終順位・得点はシステムテストにより決定します。本テストはコンテスト終了後、本テストケースとは異なる、150個のジャッジデータで最終提出をリジャッジすることで評価します。150個のジャッジデータは、テストケースと同じ方法で生成し、90個のランダムグラフ（そのうち40個は各頂点の次数が高々8）と60個の完全グラフで構成します。本テストにより、最終順位が変動するかもしれません。本テストはシード値の特定等、チューニングによる高得点を防ぐためのものであり、AtCoder社様との協議の結果、本テストにて最終順位を決定します。 ### グラフ G の生成について すべてのテストケースについて、与えられるグラフ $ G $ は「ランダムグラフ」または「完全グラフ」のいずれかです。それぞれのグラフの生成方法を以下に簡単に示します。 詳細は[サンプルコード](https://img.atcoder.jp/hokudai-hitachi2017-1/problem1_toolkit_JP_r1.zip)をご覧ください。 **ランダムグラフ** - はじめに、 $ |V| $ 頂点からなる木をランダムに生成し、その後 $ |E|\ -\ |V|\ +\ 1 $ 回ランダムに辺を張り、グラフの各辺についてランダムに重み付けします。 - ランダムグラフのうち $ 8 $ ケースは、各頂点の次数が高々 $ 8 $ であるようなランダムグラフになっています。これは新たに辺を張るときに、すでに頂点の次数が $ 8 $ である頂点を選ばないように生成しています。 **完全グラフ** - $ 1\ \leq\ u\ \lt\ v\ \leq\ |V| $ を満たすすべての $ (u,\ v) $ の組について、重み $ w $ をランダムに設定し辺を張ります。 ### ジェネレータ・テスターおよび参考文献 この問題のジェネレータおよびテスターは[ここ](https://img.atcoder.jp/hokudai-hitachi2017-1/problem1_toolkit_JP_r1.zip)からダウンロードできます。 この問題を解くにあたって、以下の文献が参考になります。こちらを参考にしながら解答を作成しても良いです。 H. Neven, et al., "NIPS 2009 demonstration: Binary classification using hardware implementation of quantum annealing." Quantum (2009): 1-17. ### Sample Explanation 2 この入力例を図示したものは以下の通りです。 !\[\](https://img.atcoder.jp/hokudai-hitachi2017-1/d08f7cdbfde51d8c34ae4da248f15613.png)