AT_hitachi2017_2_a Problem 2

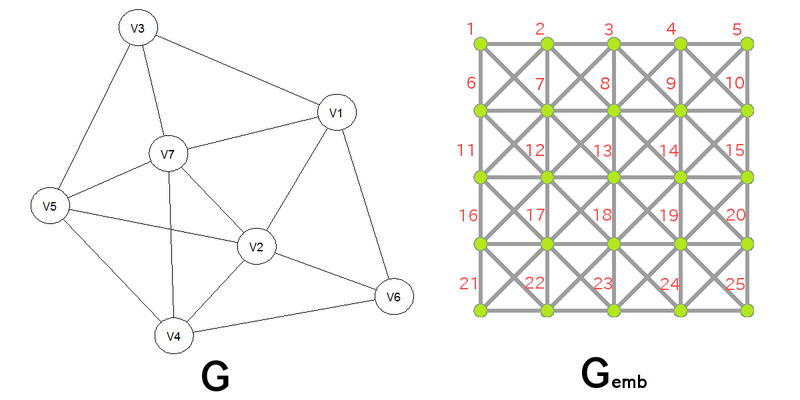
[problemUrl]: https://atcoder.jp/contests/hokudai-hitachi2017-2/tasks/hitachi2017_2_a 頂点集合 $ V $ 、辺集合 $ E $ よりなるグラフを $ G=(V,E) $ と書く。二つのグラフ $ G=(V,E) $ と $ G_{emb}=(V_{emb},E_{emb}) $ が与えられている。 下記制約のもとで、以下で説明する得点ができるだけ高くなるように、 $ V $ のすべての要素に対し $ V_{emb} $ の頂点の部分集合を対応させよ。 なお、 $ G_{emb} $ は以下の図で示すような、一行に含まれる頂点数と一列に含まれる頂点数が等しい正方形型の [King's Graph](https://en.wikipedia.org/wiki/King%27s_graph) である。King's Graph の頂点の番号付けについては、 左上が $ 1 $ であり、以降左から右に順に番号を振り、行末に到達したときは次の行から同様に順に番号を振るものとする。 

入力は以下の形式で標準入力から与えられる。入力はすべて整数値である。 > $ |V| $ $ |E| $ $ u_1 $ $ v_1 $ $ u_2 $ $ v_2 $ : $ u_{|E|} $ $ v_{|E|} $ $ |V_{emb}| $ $ |E_{emb}| $ $ a_1 $ $ b_1 $ $ a_2 $ $ b_2 $ : $ a_{|E_{emb}|} $ $ b_{|E_{emb}|} $ - $ |V| $ と $ |E| $ はグラフ $ G $ の頂点の数と辺の数を表す。 - $ u_i,\ v_i $ はグラフ $ G $ の辺についての情報であり、頂点 $ u_i $ と頂点 $ v_i $ が辺で接続されていることを表す。 - $ |V_{emb}| $ と $ |E_{emb}| $ はグラフ $ G_{emb} $ の頂点の数と辺の数を表す。 - $ a_i,\ b_i $ はグラフ $ G_{emb} $ の辺についての情報であり、頂点 $ a_i $ と頂点 $ b_i $ が辺で接続されていることを表す。

出力は以下の形式で標準出力に $ |V| $ 行で出力せよ。 > $ n_1 $ $ x_{1,1} $ $ x_{1,2} $ ... $ x_{1,n_1} $ $ n_2 $ $ x_{2,1} $ $ x_{2,2} $ ... $ x_{2,n_2} $ : $ n_{|V|} $ $ x_{|V|,1} $ $ x_{|V|,2} $ ... $ x_{|V|,n_{|V|}} $ - $ n_i $ は $ V $ の $ i $ 番目の頂点に対応する $ V_{emb} $ の部分集合の要素数 $ |s\ (i)| $ である。 - $ x_{i,j} $ は $ V $ の $ i $ 番目の頂点に対応する $ V_{emb} $ の部分集合の $ j $ 番目の要素である。

### 得点計算について 各テストケースの得点およびこの問題の得点は、以下のように計算する。 - 以下では $ V $ の $ i $ 番目の頂点に対応する $ V_{emb} $ の部分集合を$ s(i)\ ⊂\ V_{emb} $ とする。初期の持ち点 $ 5000 $ 点に以下のように加点または減点することで各テストケースの得点を計算する。 - グラフ $ G $ の各辺 $ (u,v)\ \in\ E $ に対し、$ s\ (u) $ に属する頂点 $ a\ \in\ s\ (u) $ と $ s\ (v) $ に属する頂点 $ b\ \in\ s\ (v) $ が存在し、それらがグラフ $ G_{emb} $ の辺で結ばれている、すなわち $ (a,b)\ \in\ E_{emb} $ であるとき、$ 100 $ 点を加点する。 - グラフ $ G $ のすべての辺 $ (u,v)\ \in\ E $ に対し $ 100 $ 点加点されたとき、さらに $ 100000 $ 点をボーナス点として加点する。ただし、すべてのテストケースについてボーナス点が獲得できる入力であることは保証されていない。 - 上の合計点から $ ∑\ _{u\ \in\ V}\ (|s(u)|-1) $ 点を減点したものが、各テストケースの得点となる。 - 以下の条件のいずれかに該当する場合は $ 0 $ 点となる。 1. グラフ $ G_{emb} $ から、部分集合 $ s(i)\ ⊂\ V_{emb} $ に含まれない頂点とそれに隣接する辺を全て削除してできたグラフが連結とならないものが存在する（下図の赤色の四角を参照）。 2. 異なる $ 2 $ つの部分集合 $ s(i),\ s(j) $ $ (i\ \neq\ j) $ において、共通部分が空でないものが存在する（下図の青色と紫色の四角を参照）。 3. 部分集合が空であるもの、すなわち $ |s(i)|\ =\ 0 $ となるような部分集合 $ s(i) $ が存在する。 4. 実行制限時間またはメモリを超過する、ないしは出力が正しい出力フォーマットに従っていない。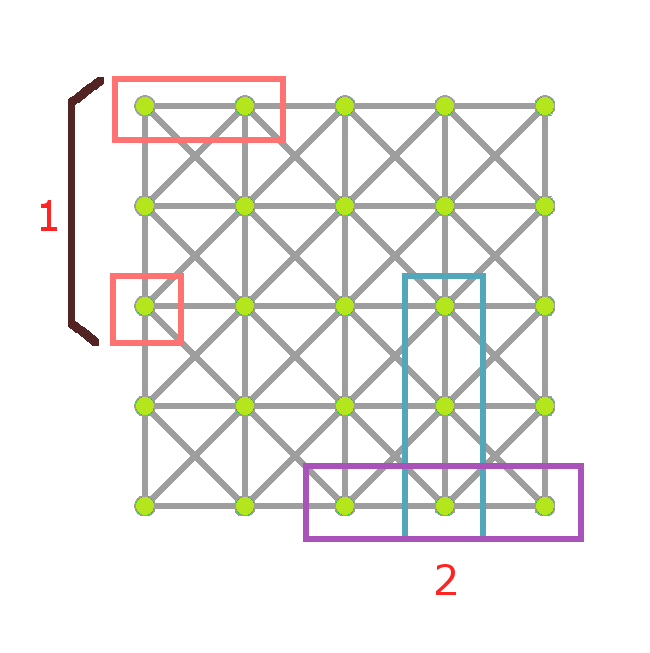 得点が $ 0 $ 点となる条件 $ 1 $ と $ 2 $ に該当する具体例 - テストケースは全部で $ 30 $ 個あり、各テストケースの得点の合計がこの問題の得点となる。 - コンテスト終了後にシステムテストを行い、この $ 30 $ 個とは別のジャッジデータ $ 150 $ 個に対する得点の合計が最終得点となる。 ### グラフ G についての制約 - $ 2\ \leq\ |V|\ \leq\ 5\ \times\ 10^2 $ - $ 1\ \leq\ |E|\ \leq\ min\ (\ \frac{|V|\ \times\ (|V|-1)}{2},\ 2\ \times\ 10^4\ ) $ - $ 1\ \leq\ u_i\ \lt\ v_i\ \leq\ |V| $ - $ i\ \neq\ j $ ならば、 $ u_i\ \neq\ u_j $ または $ v_i\ \neq\ v_j $ - 与えられるグラフは連結である。 ### グラフ G\_{emb} についての制約 - $ G_{emb} $ は正方形の King's グラフである。 - $ 4\ \leq\ |V_{emb}|\ \leq\ 3.6\ \times\ 10^3 $ かつ $ |V_{emb}| $ は平方数 - $ |V|\ \leq\ |V_{emb}| $ - $ 1\ \leq\ a_i\ \lt\ b_i\ \leq\ |V_{emb}| $ ### 出力についての制約 - 出力は $ |V| $ 行からなる - $ 1\ \leq\ n_i $ - $ 1\ \leq\ x_{i,j}\ \leq\ |V_{emb}| $ - $ i\ \neq\ j $ または $ k\ \neq\ l $ ならば $ x_{i,k}\ \neq\ x_{j,l} $ ### グラフ G の生成について すべてのテストケースについて、与えられるグラフ $ G $ は「ランダムグラフ」である。 これははじめに、 $ |V| $ 頂点からなる木をランダムに生成し、その後 $ |E|\ -\ |V|\ +\ 1 $ 回ランダムに辺を張ることで生成される。詳細は[サンプルコード](https://img.atcoder.jp/hokudai-hitachi2017-2/problem2_toolkit_JPr.zip)をご覧ください。 ### ジェネレータとテスターおよび参考文献 - この問題のジェネレータおよびテスターは[ここ](https://img.atcoder.jp/hokudai-hitachi2017-2/problem2_toolkit_JPr.zip)からダウンロードできる。 - この問題を解くにあたって、以下の文献を参考にしながら解答を作成しても良い。 [J. Cai, et al., "A practical heuristic for finding graph minors", arXiv:1406.2741 \[quant-ph\]](https://arxiv.org/abs/1406.2741) ### Sample Explanation 1 \### 出力例 1 ``` 3 14 15 20 1 19 1 9 1 23 1 18 1 25 1 13 ``` この出力例では、入力グラフ $ G $ の各頂点に対して、$ V_{emb} $ の部分集合は以下の図で対応付ける。すなわち、入力グラフの頂点の番号を $ v_1 $ から $ v_7 $ としており、各頂点に対応する $ V_{emb} $ の部分集合 $ s $ は、それぞれ同じ色で囲まれている。 !\[\](https://img.atcoder.jp/hokudai-hitachi2017-2/1a61c6bd3aaec51fa2fcce1cb95ed9d7.png) 出力例 $ 1 $ で $ V_{emb} $ に対応付けられた結果、得られる得点は以下のように計算される。 - 基本得点として $ 5000 $ 点を加点する。 - グラフ $ G_{emb} $ において保持されている辺に対して $ 11\ \times\ 100\ =\ 1100 $ 点を基本得点に加点する。 例えば、グラフ $ G $ の辺 $ (v_1,\ v_7) $ において、 $ v_1 $ に対応する $ V_{emb} $ の部分集合 $ s(v_1) $ の元である $ G_{emb} $ の頂点 $ 14 $ と、 $ v_7 $ に対応する $ V_{emb} $ の部分集合 $ s(v_7) $ の元である $ G_{emb} $ の頂点 $ 13 $ との間に辺 $ (13,\ 14) $ が存在する。 従って、辺 $ (v_1,\ v_7) $ はグラフ $ G_{emb} $ において保持されており、 $ 100 $ 点を加点する。一方、辺 $ (v_3,\ v_5) $ に対しては、各頂点に対する部分集合 $ s(v_3) $ と $ s(v_5) $ の間に辺が存在しないため、その辺に対して $ 100 $ 点を加点しない。 これをグラフ $ G $ のすべての辺に対して見たとき、保持された $ 11 $ 個の辺に対しては加点されるが、図の赤の×印で示すように、保持されなかった $ 3 $ 個の辺に対しては加点されない。 - グラフ $ G $ の辺で保持されていないものがあるため、ボーナス点 $ 100000 $ 点は加点されない。 - 各部分集合 $ s(v_1) $ から $ s(v_7) $ の要素数に対して、$ (3-1)\ +\ (1-1)\ +\ (1-1)\ +\ (1-1)\ +\ (1-1)\ +\ (1-1)\ +\ (1-1)\ =\ 2 $ 点を減点する。各括弧内の最初の項は、各部分集合の要素数を示し、ここで $ s(v_1) $ は $ 3 $ 個の要素数を持つため、$ 2 $ 点が減点される。 以上のことから、合計 $ 6098 $ 点がこのテストケースに対する得点となる。 ### Sample Explanation 2 \### 出力例 2 ``` 1 5 2 7 10 1 1 1 2 1 12 1 6 1 15 1 9 1 4 4 3 8 11 14 ``` この入力例を図示したものは以下の通りである。 !\[\](https://img.atcoder.jp/hokudai-hitachi2017-2/4b4c4c43f001b53b93acd1e7d244e0bd.png)