AT_hitachi2017_2_a Problem 2

给定两个图，$G = (V, E)$ 和 $G_{emb} = (V_{emb}, E_{emb})$。其中，$G_{emb}$ 是一个 King's Graph 的正方形图，图中顶点的编号方式是从左上角开始，按行从左到右依次编号。你需要为 $V$ 中每一个顶点找到一个 $V_{emb}$ 的子集，并使得在以下约束条件下的总得分尽可能高。

输入为一行所有整数，表示两个图的详细信息： > $|V|$ $|E|$ $u_1$ $v_1$ $u_2$ $v_2$ ... $u_{|E|}$ $v_{|E|}$ $|V_{emb}|$ $|E_{emb}|$ $a_1$ $b_1$ $a_2$ $b_2$ ... $a_{|E_{emb}|}$ $b_{|E_{emb}|}$ 其中： - $|V|$ 和 $|E|$ 分别是图 $G$ 的顶点数和边数。 - $u_i$ 和 $v_i$ 表示图 $G$ 中的一条边，这条边连接顶点 $u_i$ 和 $v_i$。 - $|V_{emb}|$ 和 $|E_{emb}|$ 分别是图 $G_{emb}$ 的顶点数和边数。 - $a_i$ 和 $b_i$ 描述图 $G_{emb}$ 中的一条边，连接了顶点 $a_i$ 和 $b_i$。

输出共 $|V|$ 行，每行描述 $V$ 中一个顶点与 $V_{emb}$ 中子集的映射关系，实现格式为： > $n_1$ $x_{1,1}$ $x_{1,2}$ ... $x_{1,n_1}$ 其中： - $n_i$ 是 $V_{emb}$ 中与 $V$ 中第 $i$ 个顶点对应的子集的大小。 - $x_{i,j}$ 是 $V_{emb}$ 中对应的子集元素。

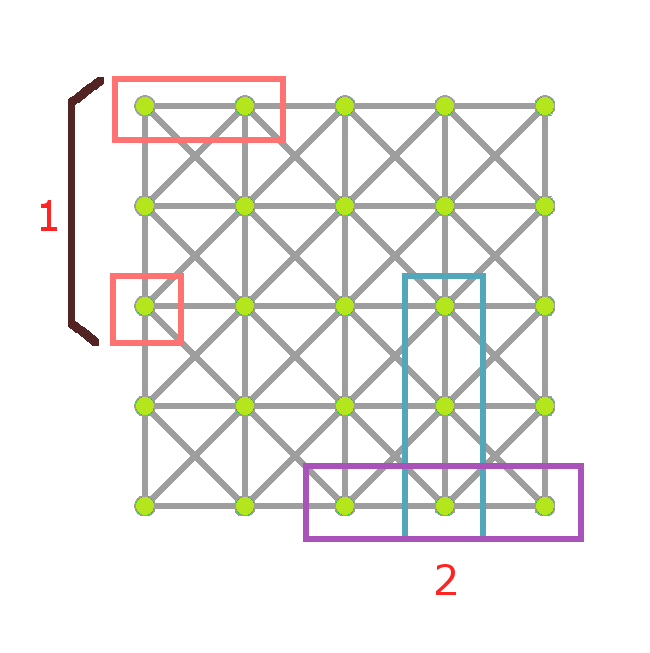
### 得分计算 每个测试用例通过以下方式进行得分计算： - 初始得分为 5000 分。 - 对于 $G$ 的每一条边 $(u, v) \in E$，如果在对应的 $s(u)$ 和 $s(v)$ 中分别找到 $a \in s(u)$ 和 $b \in s(v)$，且他们在 $G_{emb}$ 中通过边 $(a, b) \in E_{emb}$ 连接，得分增加 100 分。 - 如果所有边都符合上述条件，则额外奖励 100000 分。注意，不保证所有测试用例都能获得奖励。 - 从总得分中减去 $\sum_{u \in V} (|s(u)| - 1)$。 注意：以下任意一个情况成立，得分为 0 分： 1. 从图 $G_{emb}$ 中，删除不属于任何部分子集 $s(i) \subset V_{emb}$ 的顶点及其相邻边，若图不为连通（见红色方块示例）； 2. 存在两个不同的子集 $s(i), s(j) (i \neq j)$ 存在交集（见蓝色和紫色方块示例）； 3. 任一子集为空，即 $|s(i)| = 0$； 4. 程序超时或输出格式不正。  - 总共 30 个测试用例，累加各测试用例得分作为问题的得分。 - 赛后系统会进行额外 150 个数据的评分，总得分以这些数据得分为准。 ### 图 $G$ 的限制 - $2 \leq |V| \leq 500$ - $1 \leq |E| \leq \min\left(\frac{|V| \times (|V| - 1)}{2}, 20000\right)$ - $1 \leq u_i < v_i \leq |V|$ - 对于不同的 $i \neq j$，则条件是 $u_i \neq u_j$ 或 $v_i \neq v_j$ - $G$ 是连通图。 ### 图 $G_{emb}$ 的限制 - 是正方形的 King's Graph。 - $4 \leq |V_{emb}| \leq 3600$，且是平方数 - $|V| \leq |V_{emb}|$ - $1 \leq a_i < b_i \leq |V_{emb}|$ ### 输出的限制 - 输出需有 $|V|$ 行 - $1 \leq n_i$ - $1 \leq x_{i,j} \leq |V_{emb}|$ - 对于 $i \neq j$，或 $k \neq l$，条件是有 $x_{i,k} \neq x_{j,l}$ ### 生成图 $G$ 每个测试用例中的图 $G$ 是随机生成的。具体来说，首先随机生成一个包含 $|V|$ 个顶点的树，然后再增加 $|E| - |V| + 1$ 条随机边。 ### 参考资料与工具 - [问题的生成器和测试工具](https://img.atcoder.jp/hokudai-hitachi2017-2/problem2_toolkit_JPr.zip) - [推荐文献：J. Cai, et al., "A practical heuristic for finding graph minors", arXiv:1406.2741 \[quant-ph\]](https://arxiv.org/abs/1406.2741) **本翻译由 AI 自动生成**