AT_hokudai_hitachi2019_1_b Problem B

[problemUrl]: https://atcoder.jp/contests/hokudai-hitachi2019-1/tasks/hokudai_hitachi2019_1_b ### Input & Output Format はじめに、ジャッジ側からグラフ $ G $ と、それぞれの頂点に対する注文発生頻度 $ f_i $ と、あなたが行動する時間の最大値 $ T_{\max} $ が以下の形式で標準入力に与えられる。 > $ |V| $ $ |E| $ $ u_1 $ $ v_1 $ $ d_{u_1,\ v_1} $ $ u_2 $ $ v_2 $ $ d_{u_2,\ v_2} $ $ \vdots $ $ u_{|E|} $ $ v_{|E|} $ $ d_{u_{|E|},\ v_{|E|}} $ $ f_1 $ $ f_2 $ $ \ldots $ $ f_{|V|} $ $ T_{\max} $ - $ 1 $ 行目の $ |V| $ はグラフの頂点数、$ |E| $ はグラフの辺数を表す。 - 続く $ |E| $ 行で、グラフの辺が与えられる。$ |E| $ 行のうち $ i $ 行目は、頂点 $ u_i $ と $ v_i $ の間に距離 $ d_{u_i,\ v_i} $ の辺が存在することを表す。 - 続く $ 1 $ 行で、それぞれの頂点について新たな注文が発生する頻度が与えられる。$ i $ 番目に与えられる整数は、頂点 $ i $ に新たな注文が発生する頻度が $ f_i $ であることを表す。 - 続く $ 1 $ 行で、コンテスタント側とジャッジ側が互いに処理を行う時間の最大値 $ T_{\max} $ が与えられる。 時刻 $ t $ から $ t+1 $ へ移る際の処理を示す。まずはじめに、時刻 $ t $ に関する以下の情報が標準入力に与えられる。 > $ N_{\text{new}} $ $ \mathrm{new\_id}_1 $ $ \mathrm{dst}_1 $ $ \mathrm{new\_id}_2 $ $ \mathrm{dst}_2 $ $ \vdots $ $ \mathrm{new\_id}_{N_{\text{new}}} $ $ \mathrm{dst}_{N_{\text{new}}} $ $ N_{\text{put}} $ $ \mathrm{put\_id}_1 $ $ \mathrm{put\_id}_2 $ $ \mathrm{put\_id}_{N_{\text{put}}} $ - $ N_{\text{new}} $ は、その時刻において新たに発生した注文の数を表す。 - 続く $ N_{\text{new}} $ 行で、新たに発生した注文情報が与えられる。$ i $ 番目に与えられる注文情報は、注文 ID が $ \mathrm{new\_id}_i $ であり、その注文の発生元 (お届け先) が頂点 $ \mathrm{dst}_i $ であることを表す。 - $ N_{\text{put}} $ は、その時刻において店舗で新たに車に積まれた商品の数を表す。 - その時点で車が店舗にいなければ、$ N_{\text{put}} $ は $ 0 $ である。 - 続く $ N_{\text{put}} $ 行で、新たに車に積まれた商品に対応する注文情報が与えられる。$ i $ 番目に与えられる注文情報は、車に積まれた商品に対応する注文 ID が $ \mathrm{put\_id}_i $ であることを表す。 あなたは、時刻 $ t $ ($ 0\ \leq\ t\ \lt\ T_{\max} $) における行動を表す整数 $ \mathrm{command} $ を以下の形式で標準出力に出力しなければならない。 > $ \mathrm{command} $ ここで、$ \mathrm{command} $ は以下の形式でなければならない。 - `stay` を行う場合: `-1` と $ 1 $ 行で出力 - `move w` を行う場合: `w` と $ 1 $ 行で出力 ただし、`move w` を行う場合、$ w $ は以下の条件をすべて満たす必要がある。条件に違反している場合は `WA` (不正解) となる。 - $ w $ は $ 1\ \leq\ w\ \leq\ |V| $ を満たす整数である - 車が頂点 $ u $ 上にいる場合、$ \left\{\ u,\ w\ \right\}\ \in\ E $ が成り立つ - 車が辺 $ \left\{\ u,\ v\ \right\} $ 上にいる場合、$ w\ =\ u $ または $ w\ =\ v $ が成り立つ 時刻 $ t $ におけるあなたの行動が出力された直後に、ジャッジ側から時刻 $ t+1 $ に関する以下の情報が標準入力に与えられる。 > $ \mathrm{verdict} $ $ N_{\text{achieve}} $ $ \mathrm{achieve\_id}_1 $ $ \mathrm{achieve\_id}_2 $ $ \vdots $ $ \mathrm{achieve\_id}_{N_{\text{achieve}}} $ - $ \mathrm{verdict} $ は、時刻 $ t $ におけるあなたの行動が実行可能であるかを表す文字列であり、以下の $ 2 $ 種類のいずれかである。 - `OK`: あなたの行動が実行可能であることを表す。 - `NG`: あなたの行動が実行不可能であることを表す。この入力を受け取った場合、あなたは **プログラムを即座に終了させなければならない。** 即座に終了させた場合は `WA` (不正解) となることが保証されるが、そうでない場合の動作は未定義である。 - $ N_{\text{achieve}} $ は、その時刻において配達が完了した注文の数を表す。 - その時点で車が頂点上にいなければ、$ N_{\text{achieve}} $ は $ 0 $ である。 - 続く $ N_{\text{achieve}} $ 行で、配達が完了した注文情報が与えられる。$ i $ 番目に与えられる注文情報は、注文 ID が $ \mathrm{achieve\_id}_i $ であることを表す。 また、$ T_{\max} $ 回目の行動に対するジャッジからの入力を受け取ったあと、あなたは **プログラムを即座に終了させなければならない。**

N/A

N/A

### 問題概要 - **問題のねらい**: 本プログラミングコンテストは、買い物支援(配達)サービスの最適化をテーマとしている。本サービスを利用する顧客はそれぞれ異なる品物をお店に注文する（顧客からの注文には固有の$ \text{ID} $が割り振られる）。お店が利用できる車は一台のため、配達中に注文された商品については、お店に戻ってその商品を車に積んでから、顧客のもと商品を届けなければならない。 - **得点**: 最適化の目的は、制限時間 $ T_{\max} $ の間に「できるだけ多くの」商品を「できるだけ早く」顧客に届けることである。なお、注文は時刻 $ 0 $ から時刻 $ 0.95\ \times\ T_{\max} $ の間に発生する可能性がある。 - **諸制約**: 本コンテストでは、車に積むことのできる商品の数に制限はない。ただし、ある注文に対応する商品をお店まで取りに行き、車に積めるのは、**その商品が注文された以降の時刻に限る** ことに注意せよ。 - **問題 A**: この問題においては、注文が発生する時刻及び、注文がどの頂点で発生したかなど、注文に関する情報が事前に与えられる。 - **問題 B**: この問題においては、事前に注文に関する情報は与えられず、全ての注文は配達中にオンラインで発生する。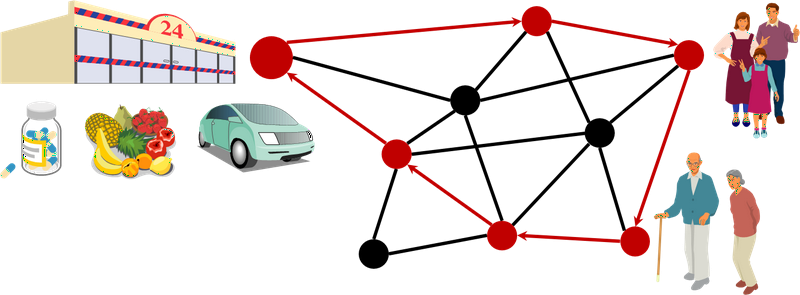  ### 時間・空間について - **時間**: $ t $ は $ 0\ \leq\ t\