AT_hokudai_hitachi2020_b hokudai_hitachi2020_b
Description
[problemUrl]: https://atcoder.jp/contests/hokudai-hitachi2020/tasks/hokudai_hitachi2020_b
Input Format
N/A
Output Format
N/A
Explanation/Hint
### 目次
[ 問題概要 ](#gaiyou)
[ タイムスケジュールと空間構造 ](#time-space)
[ ナノグリッド ](#nanogrid)
[ 電力需給 ](#yojou)
[ 運搬依頼 ](#trans)
[ EV ](#ev)
[ ナノグリッドの蓄電池の充放電処理 ](#charge)
[ 採点方法 ](#scoring)
[ 問題文 B ](#problem)
[ 入出力形式1 ](#io-format1)
[ 入出力形式2 ](#io-format2)
[ 入出力形式3 ](#io-format3)
[ 入出力制約 ](#constraints)
[ 入出力例 ](#example)
[ サンプルコード B ](#sample)
問題概要
------
この問題では、点在するナノグリッド(発電、蓄電、消費が行われる)における電力が不足しないよう、複数台のEV(=電気自動車)を用いて蓄電量のバランスを保ちつつ、人やモノをある地点から別の地点まで効率よく運搬することを考える。EVは走行距離に応じて電気を消費するため、途中でナノグリッドから充電する必要がある。ナノグリッドでは太陽光や燃料エンジンによる発電、電力の消費およびEVとの充放電が行われており、それらにより時間変動する電力需給を蓄電池の充放電および必要があれば外部からの電力供給によりバランスしている。
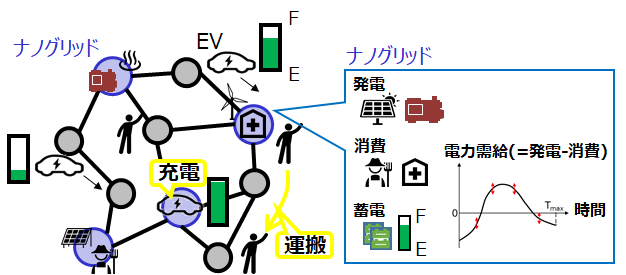
本ページ下部からダウンロード可能なtoolkitには、ジャッジからのデータ読込などI/O周りを既に実装したサンプルコードを用意しています。また、EVの動作も"all stay", "random walk", "複数同時運搬ありの輸送"などサンプルとして幾つか実装済です。新しいアルゴリズムを実装する際も、strategy classを継承する形でEVの動作の記述に注力できるつくりになっています(詳しくはREADME.mdもご参照ください)。投稿の際、こちらをご活用いただいて構いません。
タイムスケジュールと空間構造
----------------
- **タイムスケジュール**: 1つのテストケースは $ 1 $ 営業日分に相当する。時刻 $ t $ は $ 0 $ から $ T_{\max} $ までの整数の値をとる。各テストケースで天候が $ 4 $ パターンのいずれかから $ 1 $ つランダムに割り当てられ、電力需給に影響を及ぼす。コンテスタントはテストケース開始時に全時刻分の予測電力需給の情報を受け取る。また各時刻 $ t $ において、各ナノグリッドの蓄電量と、時刻 $ t $ までに発生した未配達注文の情報と、前時刻 $ t-1 $ における実際の電力需給、余剰で捨てた電力、外部からの供給電力を受け取る。これらの情報を基に、コンテスタントは時刻 $ t $ から $ t+1 $ の間に実行するEVの動作(移動、充放電、運搬など) を決定する。
- **空間構造**: 単純かつ無向であるグラフ $ G\ =\ (V,\ E) $ を考える。ここで $ V $ は頂点集合、$ E $ は辺集合である。EVの移動、充放電、及び人/モノの運搬は全てこのグラフ内で行われる。頂点のうち一定数はナノグリッドに対応する。また、辺は道路に対応し、各辺には正の整数で重み(距離)が定められている。地図を表すグラフは、後述のアルゴリズムによってランダムに生成される。
グラフ $ G $ の生成アルゴリズム 全てのテストケースにおいてグラフ $ G\ =\ (V,\ E) $ は以下のアルゴリズムによって生成される。 - **入力:**$ |V| $, $ |E| $, $ \mathrm{MaxDegree}=5 $(最大次数)
- **頂点の生成方法:**
- はじめに、$ |V|\ =\ R^{2}\ +\ r $ を満たす最大の非負整数$ R $ を見つける(ただし、$ r $ も非負整数とする)。
- 次に、$ 0\ \leq\ x,\ y\ を満たすxy $座標平面上の全ての格子点に対して、点 $ (x,\ y) $ をプロットする。
- 各点の座標を $ (x,\ y)\ \leftarrow\ (x\ +\ dx,\ y\ +\ dy) $ とずらす。ここで $ dx,\ dy $ は $ dx,\ dy\ \in\ [0,\ 1] $ を満たす一様ランダムな実数である。つまり、移動後の座標は$ (x\ +\ dx,\ y\ +\ dy)\in\ [0,R]\ \times\ [0,R] $を満たす。
- 残りの $ r $ 個の点それぞれについて、座標 $ (x',\ y') $ ($ 0\ \leq\ x',\ y'\ \leq\ R $ の一様ランダムな実数) を定めてプロットする。
- 各点に対して、$ 1 $から$ |V| $までの番号(ID)をランダムに割り振る。
- **連結性の保証:**
- 生成した頂点集合 $ u\ \in\ V $ に対して、完全グラフ $ G_{\text{comp}} $ を生成する。各頂点ペア $ u,\ v\ \in\ V\ \times\ V $ に対する頂点間のユークリッド距離を、完全グラフにおける辺の重み $ W_{u,\ v} $ と定める。
- 次に、完全グラフ $ G_{\text{comp}} $ に対して、[最小全域木](https://ja.wikipedia.org/wiki/%E5%85%A8%E5%9F%9F%E6%9C%A8#%E6%9C%80%E5%B0%8F%E5%85%A8%E5%9F%9F%E6%9C%A8) を生成し、生成された $ |V|-1 $ 本の辺を道路とする。これらの辺の重み $ d_{u,v} $ を $ d_{u,v}\ \leftarrow\ \lceil\ 2\ \times\ W_{u,\ v}\ \rceil $と定める。
- **残りの道路の作成方法:**
- 残りの $ |E|-(|V|-1) $ 本の道路は、次の手順で$ 1 $本ずつ生成される。
- $ \mathrm{cost}(u,v) $を更新する。
- グラフGの辺でつながっていない$ u $, $ v $のペアの内、$ \mathrm{cost(u,v)} $の最小を与えるペアをつなぐ辺$ \left\{\ u,\ v\ \right\} $をグラフGに加える。
- 選ばれた辺の重み $ d_{u,v} $ を $ d_{u,v}\ \leftarrow\ \lceil\ 2\ \times\ W_{u,\ v}\ \rceil $ と定める。
- ここで $ \mathrm{cost}(u,v) $ のベースは頂点間のユークリッド距離だが、低い次数の頂点が選ばれやすくなるように、また、できる限り道の交差を避けるため、斜め方向よりも縦横方向の道が選ばれやすくなるように $ \mathrm{cost}(u,v) $ を定める。以下に $ \mathrm{cost}(u,v) $ の計算方法の詳細を示す。
- 各頂点 $ u\in\ V $ の次数 $ \mathrm{degree}(u) $ を計算する。次数 $ \mathrm{degree}(u) $ は $ u\in\ V $ をいずれかの端点に含むグラフ $ G $ の辺の本数である。
- 各頂点 $ u\in\ V $ の色を、頂点の初めの(ずらす前の)座標 $ (x,y) $ をもとに、下記のように定める。まずは $ |V| $ 個の頂点のうち、$ R^{2} $ 個の頂点に対し、
- $ x+y $ が偶数の場合 : $ \mathrm{color}(u)\ =\ 0 $
- $ x+y $ が奇数の場合 : $ \mathrm{color}(u)\ =\ 1 $
- と定める。残りの $ r $ 個の頂点には、ランダムに$ 0 $もしくは$ 1 $の色を割り当てる。
- ファクター $ f(u,v) $ を以下のように定める:
- $ \mathrm{color}(u) $ と $ \mathrm{color}(v) $ が同じ場合: $ \mathrm{f}(u,v)\ =\ 5 $
- $ \mathrm{color}(u) $ と $ \mathrm{color}(v) $ が異なる場合: $ \mathrm{f}(u,v)\ =\ 1 $
- ファクター $ g(u) $ を以下のように定める:
- $ \mathrm{degree}(u)\ \lt\ \mathrm{MaxDegree} $ の場合: $ g(u)=1 $
- $ \mathrm{degree}(u)\ \geq\ \mathrm{MaxDegree} $ の場合: $ g(u)=\infty $
- $ \mathrm{cost}(u,v) $ を以下のように計算する。:
- $ \mathrm{cost}(u,v)\ =\ W_{u,v}\times\ \mathrm{degree}(u)\ \times\ \mathrm{degree}(v)\ \times\ f(u,v)\ \times\ g(u)\ \times\ g(v) $.
- **ナノグリッド頂点の選択方法:**
- 頂点集合 $ u\ \in\ V $ の中から一様ランダムに $ N_{\mathrm{grid}} $ 個の頂点を選択し、それらをナノグリッド頂点と定める。またナノグリッド頂点集合を $ V_{\mathrm{grid}} $ と表す。
ナノグリッド
--------
ナノグリッドは発電設備、電力消費者、EVの充放電設備および蓄電池から構成され、以下の内部状態を持つ。
- **頂点ID**: 頂点 $ u $ のID. ただし、$ u\ \in\ V_{\mathrm{grid}} $ ($ V_{\mathrm{grid}} $: ナノグリッド頂点集合, ("グラフ$ G $ の生成について"を参照))
- **蓄電量**: ナノグリッド内の蓄電池に蓄えられた電気の量。初期値 $ C_{\mathrm{init}}^{\mathrm{grid}} $。上限値 $ C_{\mathrm{max}}^{\mathrm{grid}} $ (初期値と上限値は全ナノグリッド共通)。各時刻 $ t $ で電力需給(=発電-消費)の値だけ増減する。また、EVと蓄電池の間の充放電によっても増減する(詳細は**[ ナノグリッドの蓄電池の充放電処理 ](#charge)**参照)。増加分が上限値 $ C_{\mathrm{max}}^{\mathrm{grid}} $ を超える場合、次の時刻 $ t+1 $ の蓄電量は上限値となり、超えた分の電気は捨てられる。逆に蓄電量が足りなくなった場合、不足分はナノグリッドの外部(系統電力)から供給され、不足分に比例してスコアは減点される(詳細は**[採点方法](#scoring)**参照)。
- **電力需給**: 各時刻におけるナノグリッド内の発電量とEVへの充電及び蓄電池への蓄電量を除いた消費量の差であり、その各時刻における予測値が時系列データで各テストケース開始時にコンテスタントに与えられる。実際の電力状態はその予測値と確率的部分(ゆらぎ、ゲリラ豪雨or想定外の晴れ)の和になる(詳細は**[電力需給](#yojou)**参照)。
- **上限充放電速度**: $ V_{\max}^{\mathrm{grid}} $. ナノグリッド内の蓄電池への充放電速度の上限値(全ナノグリッド共通)
電力需給
------
各時刻におけるナノグリッド内の発電量とEVへの充電及び蓄電池への蓄電量を除いた消費量の差である。
- **電力需給のパターン**: 1つのテストケースは $ 1 $ 営業日分($ 0\ \leq\ t\ $ S_{\mathrm{trans}} $ $ S_{\mathrm{ele}} $
入出力制約
-------
- 入力で与えられる数値のうち**"\[小数\]"**と記載されているものは小数で与えられ、その他のものは整数で与えられる。
#### 初期化(入出力形式1)
- $ N_{\mathrm{solution}}\ =\ 5 $
- $ |V|\ =\ 225 $
- $ 1.5\ |V|\ \leq\ |E|\ \leq\ 2\ |V| $
- $ 1\ \leq\ u_{i},\ v_{i}\ \leq\ |V|,\ u_i\ \ne\ v_i $ $ (1\ \leq\ i\ \leq\ |E|) $
- $ 1\ \leq\ d_i\ \leq\ \lceil\ 2\sqrt{2|V|}\ \rceil $ $ (1\ \leq\ i\ \leq\ |E|) $
- 与えられるグラフは自己ループ・多重辺が存在せず、連結であることが保証される。
- $ \mathrm{DayType}\ \in\ \left\{\ 0,\ 1,\ 2,\ 3\ \right\} $
- $ N_\mathrm{div}\ =\ 20 $
- $ N_\mathrm{pattern}\ =\ 3 $
- $ \sigma^{2}_{\mathrm{ele}}\ =\ 100 $
- $ p_{\mathrm{event}}\ \in\ \left\{\ 0.0,\ 0.1\ \right\} $ **"\[小数\]"**
- $ \Delta_{\mathrm{event}}\ =\ 1000 $
- $ -1000\ \lt\ \mathrm{pw}_{i,j}^{\mathrm{predict}}\ \lt\ 1000\ (1\ \leq\ i\ \leq\ N_\mathrm{pattern},\ 1\ \leq\ j\ \leq\ N_\mathrm{div}) $
- $ N_\mathrm{grid}\ =\ 20 $
- $ C_{\mathrm{init}}^{\mathrm{grid}}\ =\ 25000 $
- $ C_{\mathrm{max}}^{\mathrm{grid}}\ =\ 50000 $
- $ V_{\max}^{\mathrm{grid}}\ =\ 800 $
- $ 1\ \leq\ x_i\ \leq\ |V| $ $ (i\ \neq\ j $ なら $ x_i\ \neq\ x_j,\ 1\ \leq\ i\ \leq\ N_\mathrm{grid}) $
- $ 1\ \leq\ \mathrm{pattern}_i\ \leq\ N_\mathrm{pattern} $ $ (1\ \leq\ i\ \leq\ N_\mathrm{grid}) $
- $ N_{\min}^{\mathrm{EV}}\ =\ 15 $
- $ N_{\max}^{\mathrm{EV}}\ =\ 25 $
- $ N_{\min}^{\mathrm{EV}}\ \leq\ N_\mathrm{EV}\ \leq\ N_{\max}^{\mathrm{EV}} $
- $ C_{\mathrm{init}}^{\mathrm{EV}}\ =\ 12500 $
- $ C_{\mathrm{max}}^{\mathrm{EV}}\ =\ 25000 $
- $ V_{\max}^{\mathrm{EV}}\ =\ 400 $
- $ N_{\max}^{\mathrm{trans}}\ =\ 4 $
- $ \Delta_{\mathrm{move}}^{\mathrm{EV}}\ =\ 50 $
- $ 1\ \leq\ \mathrm{pos}_i\ \leq\ |V|\ (1\ \leq\ i\ \leq\ N_\mathrm{EV}) $
- $ p_{\mathrm{trans}}^{\mathrm{const}}\ =\ 0.7 $ **"\[小数\]"**
- $ T_\mathrm{last}\ =\ 900 $
- $ P^{\mathrm{trans}}\ =\ 3000 $
- $ \gamma\ =\ 2.0 $ **"\[小数\]"**
- $ S_{\mathrm{ele}}^{\mathrm{ref}}\ =\ -1,500,000 $
- $ S_{\mathrm{trans}}^{\mathrm{ref}}\ =\ -1,900,000 $
- $ T_\mathrm{max}\ =\ 1000 $
#### 繰り返し処理(入出力形式2)
- $ 1\ \leq\ x_i\ \leq\ |V| $ $ (i\ \neq\ j $ なら $ x_i\ \neq\ x_j,\ 1\ \leq\ i\ \leq\ N_\mathrm{grid}) $
- $ 0\ \leq\ y_i\ \leq\ C_{\mathrm{max}}^{\mathrm{grid}} $ $ (1\ \leq\ i\ \leq\ N_\mathrm{grid}) $
- $ -10000\ \lt\ \mathrm{pw}_{i}^{\mathrm{actual},j}\ \lt\ 10000\ (1\ \leq\ i\ \leq\ N_\mathrm{grid},\ -1\ \leq\ j\ \leq\ T_\mathrm{max}-2) $
- $ 0\ \leq\ \mathrm{pw}_{i}^{\mathrm{excess},j}\ \lt\ 10000,\ (1\ \leq\ i\ \leq\ N_\mathrm{grid},\ -1\ \leq\ j\ \leq\ T_\mathrm{max}-2) $
- $ 0\ \leq\ \mathrm{pw}_{i}^{\mathrm{buy},j}\ \lt\ 10000,\ (1\ \leq\ i\ \leq\ N_\mathrm{grid},\ -1\ \leq\ j\ \leq\ T_\mathrm{max}-2) $
- $ 0\ \leq\ \mathrm{charge}_i\ \leq\ C_{\mathrm{max}}^{\mathrm{EV}} $ $ (1\ \leq\ i\ \leq\ N_\mathrm{EV}) $
- $ 1\ \leq\ u_i,\ v_i\ \leq\ |V| $ $ (1\ \leq\ i\ \leq\ N_\mathrm{EV}) $
- $ 0\ \leq\ \mathrm{dist\_from}\_u_i\ \leq\ \lceil\ 2\sqrt{2|V|}\ \rceil $ $ (1\ \leq\ i\ \leq\ N_\mathrm{EV}) $
- $ 0\ \leq\ \mathrm{dist\_to}\_v_i\ \leq\ \lceil\ 2\sqrt{2|V|}\ \rceil $ $ (1\ \leq\ i\ \leq\ N_\mathrm{EV}) $
- $ 1\ \leq\ N_{\mathrm{adj},i}\ \leq\ 5(\mathrm{MaxDegree}) $ $ (1\ \leq\ i\ \leq\ N_\mathrm{EV}) $
- $ 1\ \leq\ a_{i,j}\ \leq\ |V| $ $ (1\ \leq\ i\ \leq\ N_\mathrm{EV},\ 1\ \leq\ j\ \leq\ N_{\mathrm{adj},i}) $
- $ 0\ \leq\ N_{\mathrm{order},i}\ \leq\ N_{\max}^{\mathrm{trans}} $ $ (1\ \leq\ i\ \leq\ N_\mathrm{EV}) $
- $ 1\ \leq\ o_{i,j}\ \leq\ T_\mathrm{last} $ $ (1\ \leq\ i\ \leq\ N_\mathrm{EV},\ 1\ \leq\ j\ \leq\ N_{\mathrm{order},i}) $
- $ 0\ \leq\ N_\mathrm{order}\ \leq\ T_\mathrm{last} $
- $ 1\ \leq\ \mathrm{id}_i\ \leq\ T_\mathrm{last} $ $ (1\ \leq\ i\ \leq\ N_\mathrm{order}) $
- $ 1\ \leq\ w_i\ \leq\ |V| $ $ (1\ \leq\ i\ \leq\ N_\mathrm{order}) $
- $ 1\ \leq\ z_i\ \leq\ |V| $ $ (1\ \leq\ i\ \leq\ N_\mathrm{order}) $
- $ w_i\ \ne\ z_i $ $ (1\ \leq\ i\ \leq\ N_\mathrm{order}) $
- $ \mathrm{state}_i\ \in\ \left\{\ 0,\ 1\ \right\} $ $ (1\ \leq\ i\ \leq\ N_\mathrm{order}) $
- $ 0\ \leq\ \mathrm{time}_i\ \leq\ T_\mathrm{last} $ $ (1\ \leq\ i\ \leq\ N_\mathrm{order}) $
#### スコア(入出力形式3)
- $ S_{\mathrm{trans}} $ **"\[小数\]"**
- $ S_{\mathrm{ele}} $ **"\[小数\]"**
入出力例
------
注意: この例はわかりやすさのために小さなセットで入出力を説明したものである。そのためパラメータの値は"入出力制約"に書かれた値とは異なるが、入出力のフォーマット(入出力形式1,2及び3)とEVの動作、及び"ナノグリッドの蓄電池の充放電処理"に書かれた計算方法は実際と同じである。
時刻 ジャッジ コンテスタント 説明 ```
1
4 4
1 2 1
2 3 2
3 4 3
4 1 1
0
2 2 1 0 10
5 -2
-4 4
2 10 20 4
1 1
4 2
2 5 10 2 2 1
2
4
0.5 3
3 0.5 -100 -100
4
```
はじめに、ジャッジ側からデータが与えられる。
$ 1 $ 行目: 求解回数は $ 1 $ 回である。
$ 2 $ 行目: 無向グラフ $ G $ は $ |V|\ =\ 4 $ 個の頂点と $ |E|\ =\ 4 $ 本の辺から構成される。
次の $ 4 $ 行 ($ 3 $ - $ 6 $ 行目) は、グラフの辺に関する情報を表す。
$ 3 $ 行目: 辺 $ 1 $ は頂点 $ 1 $ と頂点 $ 2 $ を結んでおり、長さは $ 1 $ である。
$ 4 $ 行目: 辺 $ 2 $ は頂点 $ 2 $ と頂点 $ 3 $ を結んでおり、長さは $ 2 $ である。
$ 5 $ 行目: 辺 $ 3 $ は頂点 $ 3 $ と頂点 $ 4 $ を結んでおり、長さは $ 3 $ である。
$ 6 $ 行目: 辺 $ 4 $ は頂点 $ 4 $ と頂点 $ 1 $ を結んでおり、長さは $ 1 $ である。
$ 7 $ 行目: 天候タイプは $ 0 $ "晴(ゲリラ豪雨無し)" である。
$ 8 $ 行目: 予想電力需給が一定の時間区間の数は $ 2 $ 個、ナノグリッドの需要パターンは $ 2 $ 個、電力需給のゆらぎの分散は $ 1 $ 、ゲリラ豪雨の発生確率は $ 0 $、ゲリラ豪雨発生時の電力需給の低下量は $ 10 $ である。
次の $ 2 $ 行 ($ 9 $ - $ 10 $ 行目) は、予想電力需給に関する情報を表す。
$ 9 $ 行目: 需要パターン $ 1 $ のナノグリッドの予想電力需給は $ 5 $ (時間区間 $ 1 $)、$ -2 $ (時間区間 $ 2 $)である。
$ 10 $ 行目: 需要パターン $ 2 $ のナノグリッドの予想電力需給は $ -4 $ (時間区間 $ 1 $)、$ 4 $ (時間区間 $ 2 $)である。
$ 11 $ 行目: グラフ $ G $ の頂点のうちナノグリッドがあるものは $ N_\mathrm{grid}\ =\ 2 $ 個、時刻 $ t=0 $ におけるナノグリッドの蓄電量は $ C_{\mathrm{init}}^{\mathrm{grid}}\ =\ 10 $、最大蓄電量は $ C_{\mathrm{max}}^{\mathrm{grid}}\ =\ 20 $、上限充放電速度は $ V_{\max}^{\mathrm{grid}}\ =\ 4 $ である。
$ 12 $ 行目: ナノグリッド $ 1 $ は頂点 $ 1 $ 上にあり、需要パターンは $ 1 $ である。
$ 13 $ 行目: ナノグリッド $ 2 $ は頂点 $ 4 $ 上にあり、需要パターンは $ 2 $ である。
$ 14 $ 行目: あなたが動作させることができるEVの台数は $ N_\mathrm{EV}\ =\ 2 $ 台、時刻 $ t=0 $ におけるEVの蓄電量は $ C_{\mathrm{init}}^{\mathrm{EV}}\ =\ 5 $、最大蓄電量は $ C_{\mathrm{max}}^{\mathrm{EV}}\ =\ 10 $、上限充放電速度は $ V_{\max}^{\mathrm{EV}}\ =\ 2 $ 、同時に $ 1 $ 台のEVに積載可能な運搬物の上限数は $ N_{\max}^{\mathrm{trans}}\ =\ 2 $、単位時間のEVの移動で減少する蓄電量は $ \Delta_{\mathrm{move}}^{\mathrm{EV}}\ =\ 1 $ である。
次の $ 2 $ 行 ($ 15 $ - $ 16 $ 行目) は時刻 $ t=0 $ における各EVの位置を表す。
$ 15 $ 行目: EV $ 1 $ は時刻 $ t=0 $ で頂点 $ 2 $ 上にある。
$ 16 $ 行目: EV $ 2 $ は時刻 $ t=0 $ で頂点 $ 4 $ 上にある。
$ 17 $ 行目: 各時刻で新しい運搬依頼が発生する確率は $ p_{\mathrm{trans}}^{\mathrm{const}}\ =\ 0.5 $ であり、新しい運搬依頼が発生する最終時刻は $ T_\mathrm{last}\ =\ 3 $ である。
$ 18 $ 行目: 最終時刻まで完了しない運搬依頼 $ 1 $ つあたり、$ P^{\mathrm{trans}}\ =\ 3 $ 点が減点される。ナノグリッドが外部から補充した単位電気量あたりの減点は $ \gamma\ =\ 0.5 $ 点である。電力スコアの基準スコアは $ S_{\mathrm{ele}}^{\mathrm{ref}}\ =\ -100 $ 点であり、運搬スコアの基準スコアは $ S_{\mathrm{trans}}^{\mathrm{ref}}\ =\ -100 $ 点である。
$ 19 $ 行目: あなたが行動するターン数は $ T_{\max}\ =\ 4 $ である。 0 ```
1 10 0 0 0
4 10 0 0 0
5
2 2 0 0
2 1 3
0
5
4 4 0 0
2 1 3
0
1
1 1 4 0 0
```
```
move 1
charge_from_grid 2
```
次いで、ジャッジ側から時刻 $ 0 $ でのデータが与えられる。
1 行目: 頂点 1 にあるナノグリッドの時刻 $ 0 $ での蓄電量は $ 10 $ である(時刻 $ 0 $ の場合、残りの $ 3 $ つの値は必ず $ 0 $ である)。
2 行目: 頂点 4 にあるナノグリッドの時刻 $ 0 $ での蓄電量は $ 10 $ である(時刻 $ 0 $ の場合、残りの $ 3 $ つの値は必ず $ 0 $ である)。
次の $ 4 $ 行 ($ 3 $ - $ 6 $ 行目) は、EV $ 1 $ の状態を表す。
3 行目: EV $ 1 $ の時刻 $ 0 $ での蓄電量は $ 5 $ である。
4 行目: EV $ 1 $ は時刻 $ 0 $ において頂点 $ 2 $ 上に位置する。
5 行目: EV $ 1 $ が `move` コマンドでその方向に向かって移動可能な頂点は $ N_{\mathrm{adj},1}\ =\ 2 $ 個あり、頂点 $ 1 $ および頂点 $ 3 $ である。
6 行目: EV $ 1 $ が 運搬中である注文は $ N_{\mathrm{order},i}\ =\ 0 $ 個である。
次の $ 4 $ 行 ($ 7 $ - $ 10 $ 行目) は、EV $ 2 $ の状態を表す。
7 行目: EV $ 2 $ の時刻 $ 0 $ での蓄電量は $ 5 $ である。
8 行目: EV $ 2 $ は時刻 $ 0 $ において頂点 $ 4 $ 上に位置する。
9 行目: EV $ 2 $ が `move` コマンドでその方向に向かって移動可能な頂点は $ N_{\mathrm{adj},2}\ =\ 2 $ 個あり、頂点 $ 1 $ および頂点 $ 3 $ である。
10 行目: EV $ 2 $ が 運搬中である注文は $ N_{\mathrm{order},i}\ =\ 0 $ 個である。
11 行目: 未配達の注文が $ N_\mathrm{order}\ =\ 1 $ 個存在する。
12 行目: 注文 $ 1 $ は頂点 $ 1 $ から頂点 $ 4 $ への配達であり、どのEVにも積まれておらず、時刻 $ 0 $ に発生したものである。
これに対するコンテスタントの出力は以下のとおりである。
1 行目: EV $ 1 $ を頂点 $ 1 $ の方向へ移動させようとする。EV $ 1 $ の充電が $ 1 $ 消費されるが、蓄電量が $ 1 $ 以上であったため移動は成功する。頂点 $ 1 $ から頂点 $ 2 $ への辺の長さは $ 1 $ であるので、時刻 $ 1 $ に頂点 $ 2 $ へ移動することが可能である。
2 行目: EV $ 2 $ はナノグリッドから $ 2 $ だけ充電する。EV $ 2 $ はナノグリッド上にあり、充電量はEV $ 2 $ の上限充放電速度 $ 2 $ を超えない。またEV $ 2 $ の充電後の蓄電量は最大蓄電量 $ 10 $ を超えない。したがって動作条件を満たすので、時刻 $ 1 $ に充電量を $ 7 $ に増やすことが可能である。 1 ```
1 14 5 1 0
4 6 -4 0 2
4
1 1 0 0
2 2 4
0
7
4 4 0 0
2 1 3
0
1
1 1 4 0 0
```
```
pickup 1
charge_from_grid 2
```
次いで、ジャッジ側から時刻 $ 1 $ でのデータが与えられる。
1 行目: 頂点 1 にあるナノグリッドの時刻 $ 1 $ での蓄電量は $ 14 $ であり、前時刻 $ t=0 $ における実際の電力需給、余って捨てられた電気の量、電力不足で系統から購入した電気の量がそれぞれ $ 5,\ 1,\ 0 $ である(ナノグリッドの上限充放電速度を超える分は捨てられる)。
2 行目: 頂点 4 にあるナノグリッドの時刻 $ 1 $ での蓄電量は $ 6 $ であり、前時刻 $ t=0 $ における実際の電力需給、余って捨てられた電気の量、電力不足で系統から購入した電気の量がそれぞれ $ -4,\ 0,\ 2 $ である。
次の $ 4 $ 行 ($ 3 $ - $ 6 $ 行目) は、EV $ 1 $ の状態を表す。
3 行目: EV $ 1 $ の時刻 $ 1 $ での蓄電量は $ 4 $ である。
4 行目: EV $ 1 $ は時刻 $ 1 $ において頂点 $ 1 $ 上に位置する。
5 行目: EV $ 1 $ が `move` コマンドでその方向に向かって移動可能な頂点は $ N_{\mathrm{adj},1}\ =\ 2 $ 個あり、頂点 $ 2 $ および頂点 $ 4 $ である。
6 行目: EV $ 1 $ が 運搬中である注文は $ N_{\mathrm{order},i}\ =\ 0 $ 個である。
次の $ 4 $ 行 ($ 7 $ - $ 10 $ 行目) は、EV $ 2 $ の状態を表す。
7 行目: EV $ 2 $ の時刻 $ 1 $ での蓄電量は $ 7 $ である。
8 行目: EV $ 2 $ は時刻 $ 1 $ において頂点 $ 4 $ 上に位置する。
9 行目: EV $ 2 $ が `move` コマンドでその方向に向かって移動可能な頂点は $ N_{\mathrm{adj},2}\ =\ 2 $ 個あり、頂点 $ 1 $ および頂点 $ 3 $ である。
10 行目: EV $ 2 $ が 運搬中である注文は $ N_{\mathrm{order},i}\ =\ 0 $ 個である。
11 行目: 未配達の注文が $ N_\mathrm{order}\ =\ 1 $ 個存在する。
12 行目: 注文 $ 1 $ は頂点 $ 1 $ から頂点 $ 4 $ への配達であり、どのEVにも積まれておらず、時刻 $ 0 $ に発生したものである。
これに対するコンテスタントの出力は以下のとおりである。
1 行目: 頂点 $ 1 $ に位置するEV $ 1 $ に注文 $ 1 $ を積む。充電は消費されない。
2 行目: EV $ 2 $ はナノグリッドから $ 2 $ だけ充電する。EV $ 2 $ はナノグリッド上にあり、充電量はEV $ 2 $ の上限充放電速度 $ 2 $ を超えない。またEV $ 2 $ の充電後の蓄電量は最大蓄電量 $ 10 $ を超えない。したがって動作条件を満たすので、時刻 $ 2 $ に充電量を $ 9 $ に増やすことが可能である。 2 ```
1 18 5 1 0
4 2 -4 0 2
4
1 1 0 0
2 2 4
1 1
9
4 4 0 0
2 1 3
0
2
1 1 4 1 0
2 4 1 0 2
```
```
move 4
pickup 2
```
次いで、ジャッジ側から時刻 $ 2 $ でのデータが与えられる。
1 行目: 頂点 1 にあるナノグリッドの時刻 $ 2 $ での蓄電量は $ 18 $ であり、前時刻 $ t=1 $ における実際の電力需給、余って捨てられた電気の量、電力不足で系統から購入した電気の量がそれぞれ $ 5,\ 1,\ 0 $ である。
2 行目: 頂点 4 にあるナノグリッドの時刻 $ 2 $ での蓄電量は $ 2 $ であり、前時刻 $ t=1 $ における実際の電力需給、余って捨てられた電気の量、電力不足で系統から購入した電気の量がそれぞれ $ -4,\ 0,\ 2 $ である。
次の $ 4 $ 行 ($ 3 $ - $ 6 $ 行目) は、EV $ 1 $ の状態を表す。
3 行目: EV $ 1 $ の時刻 $ 2 $ での蓄電量は $ 4 $ である。
4 行目: EV $ 1 $ は時刻 $ 2 $ において頂点 $ 1 $ 上に位置する。
5 行目: EV $ 1 $ が `move` コマンドでその方向に向かって移動可能な頂点は $ N_{\mathrm{adj},1}\ =\ 2 $ 個あり、頂点 $ 2 $ および頂点 $ 4 $ である。
6 行目: EV $ 1 $ が 運搬中である注文は $ N_{\mathrm{order},i}\ =\ 1 $ 個であり、注文 $ 1 $ を運搬中である。
次の $ 4 $ 行 ($ 7 $ - $ 10 $ 行目) は、EV $ 2 $ の状態を表す。
7 行目: EV $ 2 $ の時刻 $ 2 $ での蓄電量は $ 9 $ である。
8 行目: EV $ 2 $ は時刻 $ 2 $ において頂点 $ 4 $ 上に位置する。
9 行目: EV $ 2 $ が `move` コマンドでその方向に向かって移動可能な頂点は $ N_{\mathrm{adj},2}\ =\ 2 $ 個あり、頂点 $ 1 $ および頂点 $ 3 $ である。
10 行目: EV $ 2 $ が 運搬中である注文は $ N_{\mathrm{order},i}\ =\ 0 $ 個である。
11 行目: 未配達の注文が $ N_\mathrm{order}\ =\ 2 $ 個存在する。
12 行目: 注文 $ 1 $ は頂点 $ 1 $ から頂点 $ 4 $ への配達であり、いずれかのEV(この場合はEV $ 1 $)に積まれており、時刻 $ 0 $ に発生したものである。
13 行目: 注文 $ 2 $ は頂点 $ 4 $ から頂点 $ 1 $ への配達であり、どのEVにも積まれておらず、時刻 $ 2 $ に発生したものである。
これに対するコンテスタントの出力は以下のとおりである。
1 行目: EV $ 1 $ を頂点 $ 4 $ の方向へ移動させようとする。EV $ 1 $ の充電が $ 1 $ 消費されるが、蓄電量が $ 1 $ 以上であったため移動は成功する。頂点 $ 1 $ から頂点 $ 4 $ への辺の長さは $ 1 $ であるので、時刻 $ 3 $ に頂点 $ 4 $ へ移動することが可能である。
2 行目: 頂点 $ 4 $ に位置するEV $ 2 $ に注文 $ 2 $ を積む。充電は消費されない。 3 ```
1 17 -1 0 0
4 6 4 0 0
3
4 4 0 0
2 1 3
0
9
4 4 0 0
2 1 3
1 2
1
2 4 1 1 2
```
```
stay
move 1
```
次いで、ジャッジ側から時刻 $ 3 $ でのデータが与えられる。
1 行目: 頂点 1 にあるナノグリッドの時刻 $ 3 $ での蓄電量は $ 17 $ であり、前時刻 $ t=2 $ における実際の電力需給、余って捨てられた電気の量、電力不足で系統から購入した電気の量がそれぞれ $ -1,\ 0,\ 0 $ である(電力需給の予測値は $ -2 $ だがゆらぎにより実際の値は $ -1 $ となった)。
2 行目: 頂点 4 にあるナノグリッドの時刻 $ 3 $ での蓄電量は $ 6 $ であり、前時刻 $ t=2 $ における実際の電力需給、余って捨てられた電気の量、電力不足で系統から購入した電気の量がそれぞれ $ 4,\ 0,\ 0 $ である。
次の $ 4 $ 行 ($ 3 $ - $ 6 $ 行目) は、EV $ 1 $ の状態を表す。
3 行目: EV $ 1 $ の時刻 $ 3 $ での蓄電量は $ 3 $ である。
4 行目: EV $ 1 $ は時刻 $ 3 $ において頂点 $ 4 $ 上に位置する。
5 行目: EV $ 1 $ が `move` コマンドでその方向に向かって移動可能な頂点は $ N_{\mathrm{adj},1}\ =\ 2 $ 個あり、頂点 $ 1 $ および頂点 $ 3 $ である。
6 行目: EV $ 1 $ が 運搬中である注文は $ N_{\mathrm{order},i}\ =\ 0 $ 個である。前時刻まで積載していた注文 $ 1 $ は目的地頂点 $ 4 $ に到達したため、降ろされた。
次の $ 4 $ 行 ($ 7 $ - $ 10 $ 行目) は、EV $ 2 $ の状態を表す。
7 行目: EV $ 2 $ の時刻 $ 3 $ での蓄電量は $ 9 $ である。
8 行目: EV $ 2 $ は時刻 $ 3 $ において頂点 $ 4 $ 上に位置する。
9 行目: EV $ 2 $ が `move` コマンドでその方向に向かって移動可能な頂点は $ N_{\mathrm{adj},2}\ =\ 2 $ 個あり、頂点 $ 1 $ および頂点 $ 3 $ である。
10 行目: EV $ 2 $ が 運搬中である注文は $ N_{\mathrm{order},i}\ =\ 1 $ 個であり、注文 $ 2 $ を運搬中である。
11 行目: 未配達の注文が $ N_\mathrm{order}\ =\ 1 $ 個存在する。
12 行目: 注文 $ 2 $ は頂点 $ 4 $ から頂点 $ 1 $ への配達であり、いずれかのEV(この場合はEV $ 2 $)に積まれており、時刻 $ 2 $ に発生したものである。
これに対するコンテスタントの出力は以下のとおりである。
1 行目: EV $ 1 $ はその場にとどまる
2 行目: EV $ 2 $ を頂点 $ 1 $ の方向へ移動させようとする。EV $ 1 $ の充電が $ 1 $ 消費されるが、蓄電量が $ 1 $ 以上であったため移動は成功する。頂点 $ 4 $ から頂点 $ 1 $ への辺の長さは $ 1 $ であるので、時刻 $ 4 $ に頂点 $ 1 $ へ移動することが可能である。また、積んでいる注文 $ 2 $ の到着地点は頂点 $ 1 $ であるので、その際に注文 $ 2 $ が完了する。 4 ```
1 15 -2 0 0
4 10 5 1 0
3
4 4 0 0
2 1 3
0
8
1 1 0 0
2 2 4
0
0
3.0 34.0
```
最後に、ジャッジ側から時刻 $ 4 $ でのデータが与えられる。
1 行目: 頂点 1 にあるナノグリッドの時刻 $ 4 $ での蓄電量は $ 15 $ であり、前時刻 $ t=3 $ における実際の電力需給、余って捨てられた電気の量、電力不足で系統から購入した電気の量がそれぞれ $ -2,\ 0,\ 0 $ である。
2 行目: 頂点 4 にあるナノグリッドの時刻 $ 4 $ での蓄電量は $ 10 $ であり、前時刻 $ t=3 $ における実際の電力需給、余って捨てられた電気の量、電力不足で系統から購入した電気の量