AT_hokudai_hitachi2022_a 農機シェアリング計画最適化問題

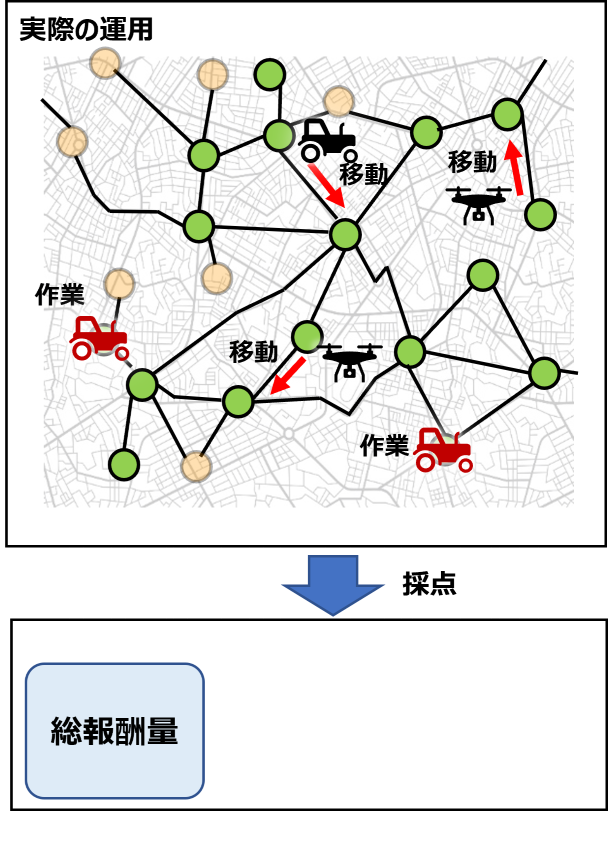
[problemUrl]: https://atcoder.jp/contests/hokudai-hitachi2022/tasks/hokudai_hitachi2022_a 本题要求在农机共享服务中，最大限度地利用所拥有的机械和人员（以下简称“工人”），以获得最多的报酬来完成农作业（以下简称“作业”）。你需要指挥工人移动和作业，处理分布在空间中的大量作业。每个作业由多个小作业“任务”组成，工人需要按规定数量完成这些任务，作业才算完成。完成作业可以获得报酬，但任务处理的时间会影响报酬，因此需要考虑合适的作业时段。此外，每个时刻工人能执行的任务数取决于其处理能力。 *报酬：假设与农作物的适宜收获期、纳米电网向农机供能的可再生能源利用率等相关。   输入首先给出以下信息： 1. 作业期间 2. 地理信息（图） 3. 工人信息 4. 所有作业信息 你需要输出： 1. 作业期间内每个时刻所有工人的行动 通过作业获得的报酬总和即为得分。 以下为详细说明。 ##

首先输入： 1. 作业期间 2. 地理信息（图） 3. 工人信息 4. 所有作业信息 具体格式如下： > $ T_{\rm{max}}\\ N_V\,\,N_E\\ u_1\quad\ v_1\quad\ d_1\\ \vdots\\ u_{N_E}\,\,\ v_{N_E}\,\,\ d_{N_E}\\ N_{\rm{worker}}\\ v^{\rm{init}}_1\,\,L^\text{max}_1\,\,N^{\rm{JobType}}_1\,\,\text{Type}^1_1\,\,\text{Type}^1_2\,\,\cdots\ \text{Type}^1_{N^{\rm{JobType}}_1}\\ \vdots\\ v^{\rm{init}}_{N_{\rm{worker}}}\,\,L^\text{max}_{N_{\rm{worker}}}\,\,N^{\rm{JobType}}_{N_{\rm{worker}}}\,\,\text{Type}^{N_{\rm{worker}}}_1\,\,\text{Type}^{N_{\rm{worker}}}_2\,\,\cdots\ \text{Type}^{N_{\rm{worker}}}_{N^{\rm{JobType}}_1}\\ N_{\rm{job}}\\ \text{Job}_1\\ \vdots\\ \text{Job}_{N_{\rm{job}}} $ （$\text{Job}_i$ 的结构见下文） #### 作业期间 - **输入** - 第 $1$ 行给出作业期间长度 $T_\text{max}$。 本题中时刻 $t$ 取 $1$ 到 $T_{\text{max}}$ 的整数值。 输入示例（$T_\text{max}=300$）： ``` 300 ``` - 第1行：作业期间长度为 `300`（$T_\text{max}=300$）。 #### 地理信息 - **输入** - 接下来1行给出地理信息图（连通的正权无向图）的顶点数 $N_V$ 和边数 $N_E$。 - 这 $N_V$ 个顶点编号为 $1$ 到 $N_V$。 - 接下来 $N_E$ 行，每行给出一条边的信息：端点 $u_i, v_i$ 及权重（距离）$d_i$。 作业分布在图的顶点上，工人在图上移动。 输入示例（$N_V=14, N_E=19$）： ``` 14 19 1 7 1 1 2 1 2 9 1 2 3 1 3 5 1 3 7 1 3 6 1 4 13 2 4 10 2 4 6 1 4 5 1 6 8 1 7 8 1 8 14 2 9 11 2 10 12 2 10 11 2 12 13 2 13 14 2 ``` - 第1行：图有 `14` 个顶点，`19` 条边（$N_V=14, N_E=19$）。 - 第2行：顶点 `1` 和 `7` 之间有长度为 `1` 的边。 - 其余各行类似。 #### 工人 工人负责执行作业，可以移动和执行任务。工人的行动由你的输出指定。 - **输入** - 接下来1行给出工人数 $N_{\text{worker}}$。 - 接下来 $N_{\text{worker}}$ 行，每行描述一个工人： - 初始位置（顶点编号）：$v^{\text{init}}_i$ - 单位时间可执行的最大任务数：$L^{\text{max}}_i$ - 可执行的作业类型数 $N^{\text{JobType}}_i$ 及类型序列 $\text{Type}^i_1\,\,\text{Type}^i_2\,\,\cdots\,\,\text{Type}^i_{N^{\text{JobType}}_i}$ 顺序即为工人ID。 每个工人的单位时间任务上限和可处理作业类型可能不同。 输入示例（$N_{\text{worker}}=5$）： ``` 5 6 100 3 1 2 3 13 59 1 3 10 55 2 2 3 9 47 3 1 2 3 9 89 1 2 ``` - 第1行：工人数为 `5`。 - 第2行：ID=1 的工人，初始位置为顶点 `6`，单位时间任务上限为 `100`，可处理类型为 `1,2,3`。 - 其余各行类似。 #### 作业 作业是工人在顶点上执行的工作。 - **作业定义** - 作业是现实中某项工作的单元，如收割、喷洒农药等。 - 作业由多个更小的“任务”组成，如采摘一个果实、收割一定面积的稻谷等。只需关注任务数量，完成规定数量即视为作业完成。 - 作业分布在地理信息图的顶点上。 - **任务处理与报酬** - 工人负责处理作业的任务。 - 你需要指挥工人移动到作业所在顶点并处理任务。 - 完成作业（即处理完规定数量的任务）即可获得报酬。 - 工人单位时间可处理的任务量有限，完成作业通常需要多时刻。 - **作业完成时获得的报酬取决于任务处理的时刻。**具体为：各时刻任务处理量 $\times$ 该时刻的单任务报酬 $r(t)$，对所有时刻求和。 - 每个作业的 $r(t)$ 可能不同。 - 所有工人获得的报酬总和即为得分。 - **作业间依赖关系** - 有些作业依赖于其他作业，只有依赖的作业全部完成后才能处理该作业的任务。 - 没有依赖的作业则无此限制。 **限制**：在报酬为0的时刻（即 $r(t)=0$），不能处理任务。 - **输入** - 接下来1行给出作业数 $N_{\text{job}}$。 - 接下来 $N_{\text{job}} \times 3$ 行，每3行描述一个作业 $\text{Job}_i$： $\text{Job}_i$ 格式如下： > $ \text{ID}^{\rm{job}}_i\,\,\text{Type}_i\,\,N^{\rm{task}}_i\,\,v^{\rm{job}}_i\\ N^{\rm{reward}}_i\,\,\ t^{\rm{reward}}_{i,1}\,\,\ y^{\rm{reward}}_{i,1}\cdots\ t^{\rm{reward}}_{i,N^{\rm{reward}}_i}\,\,\ y^{\rm{reward}}_{i,N^{\rm{reward}}_i}\\ N^{\rm{depend}}_i\,\,\ {\rm{id}}^{\rm{depend}}_{i,1}\,\,\ \cdots\ \,\,{\rm{id}}^{\rm{depend}}_{i,N^{\rm{depend}}_i} $ - 第1行 - 作业ID：$\text{ID}^{\text{job}}_i$ - 作业类型：$\text{Type}_i$ - 完成所需任务数：$N^{\text{task}}_i$ - 作业位置（顶点编号）：$v^{\text{job}}_i$ - 第2行（报酬函数 $r(t)$ 的定义） - 报酬函数控制点数：$N^{\text{reward}}_i$ - 控制点序列：$t^{\rm{reward}}_{i,1}\,\,y^{\rm{reward}}_{i,1}\,\,t^{\rm{reward}}_{i,2}\,\,y^{\rm{reward}}_{i,2}\,\cdots\,\,t^{\rm{reward}}_{i,N^{\text{reward}}_i}\,\,y^{\rm{reward}}_{i,N^{\text{reward}}_i}$ - 第3行（依赖作业） - 依赖作业数：$N^{\text{depend}}_i$ - 依赖作业ID：${\rm{id}}^{\rm{depend}}_{i,1}\,\,{\rm{id}}^{\rm{depend}}_{i,2}\,\ \cdots\ \,\,{\rm{id}}^{\rm{depend}}_{i,N^{\rm{depend}}_i}$ 报酬函数 $r(t)$ 说明：$r(t)$ 由若干控制点（时刻和值对）及其间的线性插值确定。 即，给定控制点序列 $p=((t_i,y_i))_{i=1,\cdots,n}$（$t_i,y_i\in\mathbb{Z},t_1

你需要输出每个时刻所有工人的行动，格式如下： > $ \text{Actions}_1\\ \vdots\\ \text{Actions}_{T_\text{max}} $ 每个 $\text{Actions}_i$ 为时刻 $i$ 所有工人的行动，具体为： > $ \text{action}^i_1\\ \text{action}^i_2\\ \vdots\\ \text{action}^i_{N_{\text{worker}}} $ #### 工人行动 每个工人的行动 $\text{action}$ 为字符串，分为三种： - `stay`：原地不动，不移动也不执行作业。 - `move w`：从当前位置沿最短路径向编号为 $w$ 的顶点移动一步（距离1）。 - $w$ 必须存在且与当前位置不同。 - `execute i a`：在当前位置执行ID为 $i$ 的作业 $a$ 个任务。需满足： - 工人当前位置与作业 $i$ 的位置一致。 - 作业 $i$ 的类型在工人可处理类型中。 - $a$ 为正整数，且不超过作业 $i$ 剩余任务数和工人单位时间任务上限。 - 作业 $i$ 依赖的作业全部已完成。 - 当前时刻报酬值为正。 `move w` 时，如有多条最短路径，任选一条即可。你也可通过指定中间点来选择路径。 如行动字符串不符合上述格式，判为 `WA`。 每个时刻结束时，若有作业的已处理任务数超过 $N^{\text{task}}_i$，判为 `WA` 或 `RE`。 - **输出** - 共 $N_\text{worker} \times T_\text{max}$ 行，每行一个工人行动。 输出示例（$T_\text{max}=30, N_\text{worker}=5$）： ``` move 8 stay move 13 stay stay execute 1 100 stay move 13 stay stay execute 1 100 stay move 13 move 1 stay execute 1 100 stay move 13 move 1 stay execute 1 100 stay move 13 move 1 stay execute 1 100 stay move 13 execute 7 47 stay execute 1 100 stay execute 4 55 execute 7 47 stay execute 1 25 move 14 execute 4 55 execute 7 47 stay stay move 14 execute 4 55 execute 7 47 stay stay move 14 execute 4 55 execute 7 47 stay stay move 14 execute 4 55 execute 7 47 stay stay move 14 execute 4 55 execute 7 47 stay stay move 14 execute 4 55 execute 7 47 stay stay move 14 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay execute 2 59 execute 4 55 execute 7 47 stay stay stay execute 4 55 execute 7 47 stay stay stay stay execute 7 47 stay stay stay stay execute 7 47 stay ``` - 每 $N_\text{worker}$ 行为一个时刻所有工人的行动。 ##

#### 评分方法 得分 $S$ 按如下公式计算： $$ S = \left\lfloor \sum_{j\in J_\text{finished}} \sum_{w\in W} \sum_{t=1}^{T_\text{max}} a^w_j(t) r_j(t) \right\rfloor $$ - $J_\text{finished}$：已完成的作业集合 - $W$：所有工人集合 - $a^w_j(t)$：时刻 $t$ 工人 $w$ 执行作业 $j$ 的任务数 - $r_j(t)$：时刻 $t$ 作业 $j$ 的单任务报酬 $\left\lfloor x \right\rfloor$ 表示不超过 $x$ 的最大整数（向下取整）。 #### 约束条件 - $300 \leq T_\text{max} \leq 1000$，且 $T_\text{max}$ 为 $100$ 的倍数。 - $150 \leq N_V \leq 2000$ - $4N_V/3 \leq N_E \leq 2N_V$ - $1 \leq u_i, v_i \leq N_V, u_i \neq v_i$ - $1 \leq d_i \leq 128$ - 图无自环、无重边，且连通。 - $1 \leq N_\text{worker} \leq 10$ - $1 \leq v^\text{init}_i \leq N_V$ - $30 \leq L^\text{max}_i \leq 100$ - $1 \leq N^\text{JobType}_i \leq 3$ - $1 \leq \text{Type}^i_j \leq 3$ - $250 \leq N_\text{job} \leq 1003$ - $\text{ID}^\text{job}_i = i$ - $1 \leq \text{Type}_i \leq 3$，且至少有一个工人能处理该类型。 - $500 \leq N^\text{task}_i \leq 1500$ - $1 \leq v^\text{job}_i \leq N_V$ - $1 \leq N^\text{reward}_i \leq 43$ - $0 \leq t^\text{reward}_{i,1} < t^\text{reward}_{i,2} < \cdots < t^\text{reward}_{i,N^\text{reward}_i} \leq T_\text{max}+1$ - $y^\text{reward}_{i,1}=y^\text{reward}_{i,N^\text{reward}_i}=0, 1 \leq y^\text{reward}_{i,j} \leq 10^7$ - $0 \leq N^\text{depend}_i \leq 3$ - $1 \leq \text{id}^\text{depend}_{i,j} \leq N_\text{job}$，依赖ID不重复且不为自身 - 作业依赖关系构成有向无环图（DAG），每个连通分量大小不超过4 #### 其它说明 - 工人行动字符串需严格符合格式，否则判为错误。 - 每个时刻结束时，任何作业的已处理任务数不得超过所需任务数。 - 评分时，只有已完成的作业才计入得分。 - 详细的测试数据生成规则、评分细则、可视化工具等请参见原文链接及工具包说明。 由 ChatGPT 4.1 翻译