AT_hokudai_hitachi2022_a 農機シェアリング計画最適化問題

[problemUrl]: https://atcoder.jp/contests/hokudai-hitachi2022/tasks/hokudai_hitachi2022_a

N/A

N/A

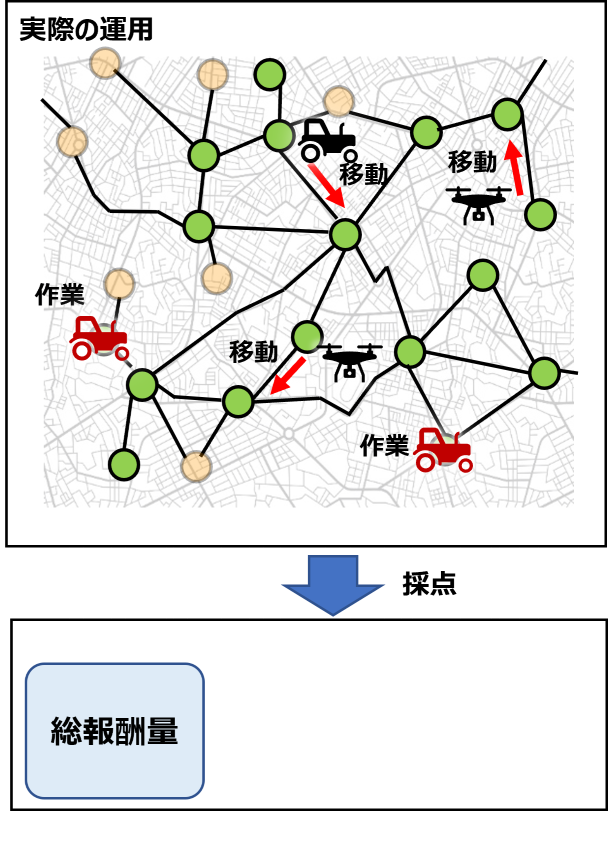
### 問題概要 この問題では、農機シェアリングサービスにおいて、所有する機械や人員（単純化して、以下"ワーカー"とする）を最大限活用し、報酬\*が最も多くなるように農作業（以下、"ジョブ"と呼ぶ）を 処理することを考える。ワーカーに移動と作業の指示を出し、空間内に配置された数多く存在するジョブを処理していく。各ジョブは複数の小作業を表す"タスク"をワーカーが規定の量処理することで完了と見なされる。ジョブを完了することで報酬を獲得できるが、タスクを処理する時刻により報酬量は異なるため適切な作業時間帯を考慮して処理する必要がある。また、各時刻における実行可能なタスク数はワーカーの処理能力に依存する。 \*報酬：農作物の適切な収穫時期、ナノグリッドから農機に供給する再生可能エネルギーの利用率等を想定する。   入力として最初に以下の情報が与えられる。 1. 作業期間 2. 地理情報（グラフ） 3. ワーカーの情報 4. 全てのジョブの情報 これに対しコンテスタントは 1. 作業期間内の全ての時刻におけるワーカーの行動 を出力する。 作業により得られた報酬の総和がスコアとなる。 以下はその詳細である。 ### 入力1 最初に入力として 1. 作業期間 2. 地理情報（グラフ） 3. ワーカーの情報 4. 全てのジョブの情報 が以下の形式で標準入力から与えられる。 > $ T_{\rm{max}}\\ N_V\,\,N_E\\ u_1\quad\ v_1\quad\ d_1\\ \vdots\\ u_{N_E}\,\,\ v_{N_E}\,\,\ d_{N_E}\\ N_{\rm{worker}}\\ v^{\rm{init}}_1\,\,L^\text{max}_1\,\,N^{\rm{JobType}}_1\,\,\text{Type}^1_1\,\,\text{Type}^1_2\,\,\cdots\ \text{Type}^1_{N^{\rm{JobType}}_1}\\ \vdots\\ v^{\rm{init}}_{N_{\rm{worker}}}\,\,L^\text{max}_{N_{\rm{worker}}}\,\,N^{\rm{JobType}}_{N_{\rm{worker}}}\,\,\text{Type}^{N_{\rm{worker}}}_1\,\,\text{Type}^{N_{\rm{worker}}}_2\,\,\cdots\ \text{Type}^{N_{\rm{worker}}}_{N^{\rm{JobType}}_1}\\ N_{\rm{job}}\\ \text{Job}_1\\ \vdots\\ \text{Job}_{N_{\rm{job}}} $ ($ \text{Job}_i $の構成は後述) #### 作業期間 - **入力** - 最初の$ 1 $行目で作業期間の長さ$ T_\text{max} $が与えられる。 この問題における時刻$ t $は $ 1 $ から $ T_{\text{max}} $までの整数の値をとる。 入力例 以下は $ T_\text{max}=300 $の例: ``` 300 ``` (末尾に改行有) - 1行目:作業期間の長さは`300` である。($ T_\text{max}=300 $) #### 地理情報 - **入力** - 次の$ 1 $行で、問題の地理情報を表すグラフ(連結な正の重み付き無向グラフ)の頂点数$ N_V $と辺の数$ N_E $が与えられる。 - この$ N_V $個の頂点には$ 1 $から順に$ N_V $まで頂点番号が割り当てられるものとする。 - 続く$ N_E $行で辺を表す情報: 端点$ u_i,v_i $と重み(=距離)$ d_i $ が与えられる。($ 1\leq\ i\ \leq\ N_E $) 後述するが、[ジョブ](#job)はこのグラフの頂点上に配置され、[ワーカー](#worker)はこのグラフの上を移動する。 入力例 以下は $ N_V=14,N_E=19 $の例: ``` 14 19 1 7 1 1 2 1 2 9 1 2 3 1 3 5 1 3 7 1 3 6 1 4 13 2 4 10 2 4 6 1 4 5 1 6 8 1 7 8 1 8 14 2 9 11 2 10 12 2 10 11 2 12 13 2 13 14 2 ``` (末尾に改行有) - 1行目:グラフの頂点は`14`個存在し、辺は`19`個存在する。($ N_V=14,N_E=19 $) - この`14`個の頂点には$ 1 $から順に`14`まで頂点番号が割り当てられている。 - 以下、頂点番号$ i $に対応する頂点 を単に 頂点$ i $ と呼ぶ。 - 2行目:頂点`1`と頂点`7`の間に長さ`1`の辺が存在する。($ u_{1}=1,v_{1}=7,d_{1}=1 $) - 3行目:頂点`1`と頂点`2`の間に長さ`1`の辺が存在する。($ u_{2}=1,v_{2}=2,d_{2}=1 $) - 4行目:頂点`2`と頂点`9`の間に長さ`1`の辺が存在する。($ u_{3}=2,v_{3}=9,d_{3}=1 $) - 5行目:頂点`2`と頂点`3`の間に長さ`1`の辺が存在する。($ u_{4}=2,v_{4}=3,d_{4}=1 $) - 6行目:頂点`3`と頂点`5`の間に長さ`1`の辺が存在する。($ u_{5}=3,v_{5}=5,d_{5}=1 $) - 7行目:頂点`3`と頂点`7`の間に長さ`1`の辺が存在する。($ u_{6}=3,v_{6}=7,d_{6}=1 $) - 8行目:頂点`3`と頂点`6`の間に長さ`1`の辺が存在する。($ u_{7}=3,v_{7}=6,d_{7}=1 $) - 9行目:頂点`4`と頂点`13`の間に長さ`2`の辺が存在する。($ u_{8}=4,v_{8}=13,d_{8}=2 $) - 10行目:頂点`4`と頂点`10`の間に長さ`2`の辺が存在する。($ u_{9}=4,v_{9}=10,d_{9}=2 $) - 11行目:頂点`4`と頂点`6`の間に長さ`1`の辺が存在する。($ u_{10}=4,v_{10}=6,d_{10}=1 $) - 12行目:頂点`4`と頂点`5`の間に長さ`1`の辺が存在する。($ u_{11}=4,v_{11}=5,d_{11}=1 $) - 13行目:頂点`6`と頂点`8`の間に長さ`1`の辺が存在する。($ u_{12}=6,v_{12}=8,d_{12}=1 $) - 14行目:頂点`7`と頂点`8`の間に長さ`1`の辺が存在する。($ u_{13}=7,v_{13}=8,d_{13}=1 $) - 15行目:頂点`8`と頂点`14`の間に長さ`2`の辺が存在する。($ u_{14}=8,v_{14}=14,d_{14}=2 $) - 16行目:頂点`9`と頂点`11`の間に長さ`2`の辺が存在する。($ u_{15}=9,v_{15}=11,d_{15}=2 $) - 17行目:頂点`10`と頂点`12`の間に長さ`2`の辺が存在する。($ u_{16}=10,v_{16}=12,d_{16}=2 $) - 18行目:頂点`10`と頂点`11`の間に長さ`2`の辺が存在する。($ u_{17}=10,v_{17}=11,d_{17}=2 $) - 19行目:頂点`12`と頂点`13`の間に長さ`2`の辺が存在する。($ u_{18}=12,v_{18}=13,d_{18}=2 $) - 20($ =1+N_E $)行目:頂点`13`と頂点`14`の間に長さ`2`の辺が存在する。($ u_{19}=13,v_{19}=14,d_{19}=2 $) #### ワーカー ワーカーはジョブを処理する存在であり、移動とタスクの実行が可能である。これはコンテスタントの入力により操作される。([ワーカーの行動](#worker-action)を参照) - **入力** - 続く$ 1 $行でワーカーの数$ N_{\text{worker}} $が与えられる。 - 次の$ N_{\text{worker}} $行で各ワーカーの構成情報: - 初期位置(頂点番号): $ v^{\text{init}}_i $ - 単位時間に実行可能なタスク数の上限: $ L^{\text{max}}_i $ - 実行可能なジョブのタイプ数 $ N^{\text{JobType}}_i $ と タイプの列 $ \text{Type}^i_1\,\,\text{Type}^i_2\,\,\cdots\,\,\text{Type}^i_{N^{\text{JobType}}_i} $ が与えられる。($ 1\leq\ i\ \leq\ N_{\text{worker}} $) この入力における順序はワーカーのIDに対応する。 ワーカーごとに、単位時間に実行可能なタスク数の上限 や 処理できるジョブのタイプは異なる。 入力例 以下は $ N_{\text{worker}}=5 $ の例: ``` 5 6 100 3 1 2 3 13 59 1 3 10 55 2 2 3 9 47 3 1 2 3 9 89 1 2 ``` (末尾に改行有) - 1行目:ワーカーの数は`5`である。($ N_{\text{worker}}=5 $) - 2行目:ID=1であるワーカーの記述。 - 初期位置は頂点番号`6`に対応する頂点である。($ v^{\text{init}}_1=6 $) - 単位時間あたりに実行可能なタスク数の上限は`100`である。($ L^{\text{max}}_1=100 $) - 実行可能なジョブのタイプは`3`つあり($ N^{\text{JobType}}_1=3 $)、それらは`1`と`2`と`3`である。($ \text{Type}^1_1=1,\text{Type}^1_2=2,\text{Type}^1_3=3 $) - 3行目:ID=2であるワーカーの記述。 - 初期位置は頂点番号`13`に対応する頂点である。($ v^{\text{init}}_2=13 $) - 単位時間あたりに実行可能なタスク数の上限は`59`である。($ L^{\text{max}}_2=59 $) - 実行可能なジョブのタイプは`1`つあり($ N^{\text{JobType}}_2=1 $)、それは`3`である。($ \text{Type}^2_1=3 $) - 4行目:ID=3であるワーカーの記述。 - 初期位置は頂点番号`10`に対応する頂点である。($ v^{\text{init}}_3=10 $) - 単位時間あたりに実行可能なタスク数の上限は`55`である。($ L^{\text{max}}_3=55 $) - 実行可能なジョブのタイプは`2`つあり($ N^{\text{JobType}}_3=2 $)、それらは`2`と`3`である。($ \text{Type}^3_1=2,\text{Type}^3_2=3 $) - 5行目:ID=4であるワーカーの記述。 - 初期位置は頂点番号`9`に対応する頂点である。($ v^{\text{init}}_4=9 $) - 単位時間あたりに実行可能なタスク数の上限は`47`である。($ L^{\text{max}}_4=47 $) - 実行可能なジョブのタイプは`3`つあり($ N^{\text{JobType}}_4=3 $)、それらは`1`と`2`と`3`である。($ \text{Type}^4_1=1,\text{Type}^4_2=2,\text{Type}^4_3=3 $) - 6($ =1+N_{\text{worker}} $)行目:ID=5であるワーカーの記述。 - 初期位置は頂点番号`9`に対応する頂点である。($ v^{\text{init}}_5=9 $) - 単位時間あたりに実行可能なタスク数の上限は`89`である。($ L^{\text{max}}_5=89 $) - 実行可能なジョブのタイプは`1`つあり($ N^{\text{JobType}}_5=1 $)、それは`2`である。($ \text{Type}^5_1=2 $) #### ジョブ ジョブは頂点上でワーカーが実行する仕事である。 - **ジョブとは** - **ジョブ**は現実における作業の1つの単位に相当し、例えば作物の収穫や農薬の散布等である。 - これらはより小さな単位の複数作業から構成される。例えば、果実1つを摘み取る、稲を一定面積刈り取る、農薬を一定面積に撒く、といったものである。このようにジョブを構成する小さな単位の作業をここでは**タスク**と呼ぶことにする。 - ジョブを構成するタスクが全て一定量行われることでそのジョブは完了すると考える。 - 現実的にはジョブは複数種類のタスクから構成されるかもしれないが、今回は単純化しタスクをこなす量だけに着目する。すなわち、**タスクを規定の量処理することでジョブが完了したとみなす**ことにする。 - ジョブが行われる場所はそのジョブ毎に異なる。この問題ではそれを[地理情報](#geo-data)として与えられた**グラフの頂点上にジョブを配置**することで表現する。 - **タスクの処理と報酬** - 各ジョブのタスクを処理するものとして**[ワーカー](#worker)**が存在する。 - コンテスタントは各ワーカーに**移動**や**作業**の指示を出し、ジョブが存在する頂点に移動させタスクを処理する。 - コンテスタントは**ジョブを完了する(=タスクを規定の量処理する)ことで報酬を得る**。 - ワーカーは単位時間あたりに処理できるタスク量に上限([$ L^{\text{max}} $](#worker))があり、ジョブを完了するにはある程度時間がかかる。典型的には、ある時刻から一定時間、毎時刻タスクを一定量処理することになる。 - **ジョブ完了時に得られる報酬はタスクを処理した時刻によって異なる**。具体的には:各時刻におけるタスク処理量あたりの報酬量$ r(t) $ $ \times $ その時刻に処理されたタスク量 の時間に関する総和($ t=1,2,\cdots,T_\text{max} $)である。 - 各時刻におけるタスク処理量あたりの報酬量$ r(t) $は**ジョブ毎にも異なる。** - 全ワーカーが集めた報酬の総和がこの問題のスコアを構成する中心的な要素である。([採点方法](#scoring-method)) コンテスタントはこの報酬の総和が大きくなるようにワーカーの行動を決定する。 - **ジョブ間の依存関係** - ジョブは他のジョブに依存する場合がある。すなわち、そのジョブが依存するジョブが全て完了していなければそのジョブのタスクを処理することができないという制限がある。 - 依存するジョブが存在しない場合このような制限は無い。 各種制限- 報酬が獲得できない時刻(タスク処理量あたりの報酬量 = 0 である時刻)にはタスクを処理することができない。 - **入力** - 続く$ 1 $行でジョブの数$ N_{\text{job}} $が与えられる。 - 次の行からジョブの構成情報$ \text{Job}_i $が$ N_{\text{job}} $個与えられる。(合計$ N_{\text{job}}\times\ 3 $行) ジョブの構成情報$ \text{Job}_i $は次の形式で与えられる。 > $ \text{ID}^{\rm{job}}_i\,\,\text{Type}_i\,\,N^{\rm{task}}_i\,\,v^{\rm{job}}_i\\ N^{\rm{reward}}_i\,\,\ t^{\rm{reward}}_{i,1}\,\,\ y^{\rm{reward}}_{i,1}\cdots\ t^{\rm{reward}}_{i,N^{\rm{reward}}_i}\,\,\ y^{\rm{reward}}_{i,N^{\rm{reward}}_i}\\ N^{\rm{depend}}_i\,\,\ {\rm{id}}^{\rm{depend}}_{i,1}\,\,\ \cdots\ \,\,{\rm{id}}^{\rm{depend}}_{i,N^{\rm{depend}}_i} $ - 1行目 - ジョブID: $ \text{ID}^{\text{job}}_i $ - ジョブタイプ: $ \text{Type}_i $ - 完了までのタスク数: $ N^{\text{task}}_i $ - ジョブの位置(頂点番号): $ v^{\text{job}}_i $ - 2行目(報酬関数$ r(t) $の定義) - 報酬関数の制御点個数:$ N^{\text{reward}}_i $ - 制御点の列:$ t^{\rm{reward}}_{i,1}\,\,y^{\rm{reward}}_{i,1}\,\,t^{\rm{reward}}_{i,2}\,\,y^{\rm{reward}}_{i,2}\,\,\cdots\,\,t^{\rm{reward}}_{i,N^{\text{reward}}_i}\,\,y^{\rm{reward}}_{i,N^{\text{reward}}_i} $ - 3行目(依存するジョブ) - 依存するジョブの数: $ N^{\text{depend}}_i $ - 依存するジョブID: $ {\rm{id}}^{\rm{depend}}_{i,1}\,\,{\rm{id}}^{\rm{depend}}_{i,2}\,\,\ \cdots\ \,\,{\rm{id}}^{\rm{depend}}_{i,N^{\rm{depend}}_i} $ 報酬関数$ r(t) $の詳細 時刻$ t $におけるタスク当たりの報酬を与える関数$ r(t) $は、1個以上の制御点(時刻と値のペア)とそれらの間の線形補間で定める。 すなわち、制御点の列$ p=((t_i,y_i))_{i=1,\cdots,n} $ ($ t_i,y_i\in\ \mathbb{Z},t_1\ \ M $を満たす場合、`8.`に進む。満たさない場合`4.`に戻る。 8. $ U $に属する全ての矩形の**辺の**和集合$ A $を重み付き無向グラフ$ G=(V,E),W:E\rightarrow\ \mathbb{R}_{\ >\ 0} $とみなす。 - グラフの頂点集合$ V $は辺の和集合$ A $上において直交する線分が存在する点全て。 - グラフの辺集合$ E $は頂点のペア$ \{a,b\} $のうち、$ a\neq\ b $かつ辺の和集合$ A $上において$ a $から$ b $へ他の頂点を経由せず到達できるもの全て。 - 重み(関数)$ W $は点同士のユークリッド距離で定める。 9. この$ G=(V,E) $(重み$ W $)を地理情報の生成に使用するグラフとして採用する。 (Reference:Eisenstat, D., Random road networks: the quadtree model, Proceeding of the 8th Workshop on Analytic Algorithms and Combinatorics (ANALCO), pp.76-84, 2011 (DOI:)) - **生成手順2**(標高の生成) 1. 正方形領域$ R=[0,1024]\times[0,1024] $を用意する。 2. $ R $を$ x $方向$ y $方向共に$ 128 $分割する(=サイズ$ 8\times8 $の正方形領域$ 128\times128 $個に分割する。) 3. $ R $からランダムな正方形領域を$ 20 $個選びその和集合を$ A $とする。 4. 再び$ R $からランダムな正方形領域を$ 20 $個選びその和集合を$ B $とする。 5. 以下の偏微分方程式(を上記`2.`の分割により離散化したもの)を時刻$ t=100000 $まで解く(=$ u(100000,x,y) $を計算する): $ \displaystyle \frac{\partial\ u}{\partial\ t}=\Delta\ u-b(x,y)u+a(x,y) $ ただし、時刻$ t=0 $における初期値は$ u(0,x,y)=u_0(x,y)\equiv\ 0 $, 境界条件はノイマン境界条件で、 $ a(x,y)=\begin{cases} 1/8^2,\ &\ \text{if}\ (x,y)\ \in\ A,\ \\ 0,\ &\ \text{otherwise}, \end{cases} $ $ b(x,y)=\begin{cases} 1/8^2,\ &\ \text{if}\ (x,y)\ \in\ B,\ \\ 0,\ &\ \text{otherwise}. \end{cases} $ である。 6. $ u(100000,x,y) $を$ [0,1] $の範囲に正規化し、それを標高$ e(x,y) $として採用する。 - **生成手順3**(グラフの切断、距離スケーリング) 1. 生成手順2で生成した標高$ e(x,y) $のデータをグラフの空間サイズ$ [0,L]\times[0,L] $に合わせる。 すなわち、空間スケーリングされた標高$ \tilde\ e(x,y) $を$ \tilde\ e(x,y)=\ e(L\times\ x/1024,L\times\ y/1024) $と定める。 2. $ \tilde\ e(x,y) $がある実数$ z $より大きい部分を返す関数$ H(z)=\{(x,y)\ \in\ [0,L]\times[0,L]|\tilde\ e(x,y)\ >\ z\} $に対して、$ H(z) $の面積が$ C\times\ L^2 $以上となるような$ z $のうち最大のものを$ h $とする。 3. 生成手順1で生成したグラフの辺集合$ E $について、辺の端点(2つある)の標高がどちらも$ h $を下回るものを全て$ E $から削除する。 4. グラフ$ G=(V,E) $の最大の連結成分を$ G'=(V',E') $とする。 5. 重み$ W':E'\ \rightarrow\ \mathbb{R}_{\ >\ 0}: $を次のように定める:$ W'(e)=\ s\times\ W(e)/\min_{e'\ \in\ E'}W(e') $ 6. グラフ$ G'=(V',E') $(重み(距離)$ W' $)を地理情報として採用する。 報酬を表す区分線形関数 この問題では各時刻における報酬（正確にはタスク当たりの報酬値）を表す関数を有限個の点の線形補間で表現する。その点をここでは制御点と呼び、以下はその有限個の制御点の生成規則である。 - パラメータ - 報酬が正である区間長:$ L\geq\ 1 $ - 区間を細分する長さ:$ l\geq\ 1 $ - 報酬基準値:$ s\ >\ 0 $ - 制御点の値生成時に使用する標準偏差:$ \sigma'\ >\ 0 $ - 報酬上限値:$ M\ >\ 0 $ - 報酬下限値:$ m\ >\ 0 $ $ ~ $ 1. 報酬開始時刻$ b=\text{randint}(1,T_\text{max}-L) $、報酬終了時刻$ e=b+L $、区間分割数$ d=\text{round}(L/l) $と定める。ただし、$ \text{randint}(m,n) $は$ m $以上$ n $以下の整数を一様にランダムに選ぶ関数、$ \text{round}(x) $は$ x $を四捨五入により丸めた整数値を返す関数とする。 2. $ \mu=0,\sigma=\sigma' $である対数正規分布に従う乱数を独立に$ d+1 $個生成し$ \{c_i\}_{i=1}^{d+1} $とおく。 3. $ \{v_i\}_{i=1}^{d+1} $を $ v_i=\prod_{j=1}^{i}c_j $で定める。 4. $ B=s\sqrt{(d+1)/\sum_{i=1}^{d+1}v_i^2} $として、$ \{r_i\}_{i=1}^{d+1} $を $ r_i=\text{round}(Bv_i) $で定める。 5. $ r_i\ >\ M $または$ r_i\