AT_hokudai_hitachi2022_b 農機シェアリング計画動的最適化問題

[problemUrl]: https://atcoder.jp/contests/hokudai-hitachi2022/tasks/hokudai_hitachi2022_b

N/A

N/A

### 問題概要 この問題では、農機シェアリングサービスにおいて、所有する機械や人員（単純化して、以下"ワーカー"とする）を最大限活用し、報酬\*が最も多くなるように農作業（以下、"ジョブ"と呼ぶ）を 受託することを考える。空間内に配置された数多く存在するジョブから受託するジョブを自分で最初に決定し、ジョブ実行スケジュールを提出/修正しながら、ワーカーに指示を出し実際にそれらを処理していく。各ジョブは複数の小作業を表す"タスク"をワーカーが規定の量処理することで完了と見なされ、基本的に受託したジョブは完了する必要がある(完了しなければペナルティが発生する）。ジョブを完了することで報酬を獲得できるが、タスクを処理する時刻により報酬量は異なるため適切な作業時間帯を考慮して処理する必要がある。また、各時刻における実行可能なタスク数はワーカーの処理能力と天候に依存し、天候は一定時間ごとに予報が与えられる。 \*報酬：農作物の適切な収穫時期、ナノグリッドから農機に供給する再生可能エネルギーの利用率等を想定する。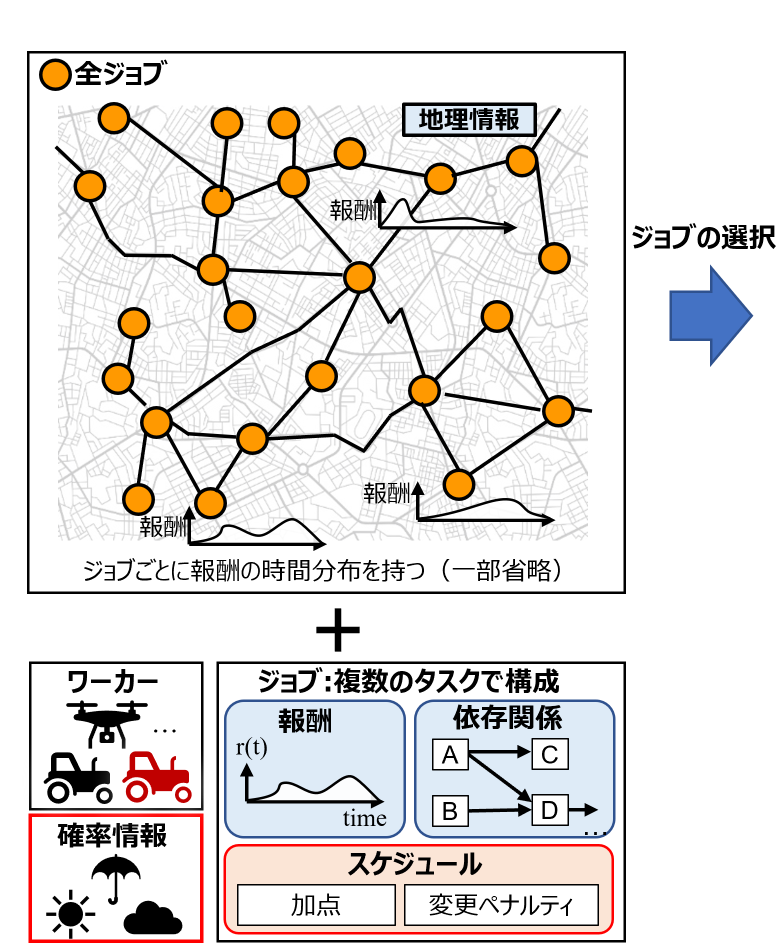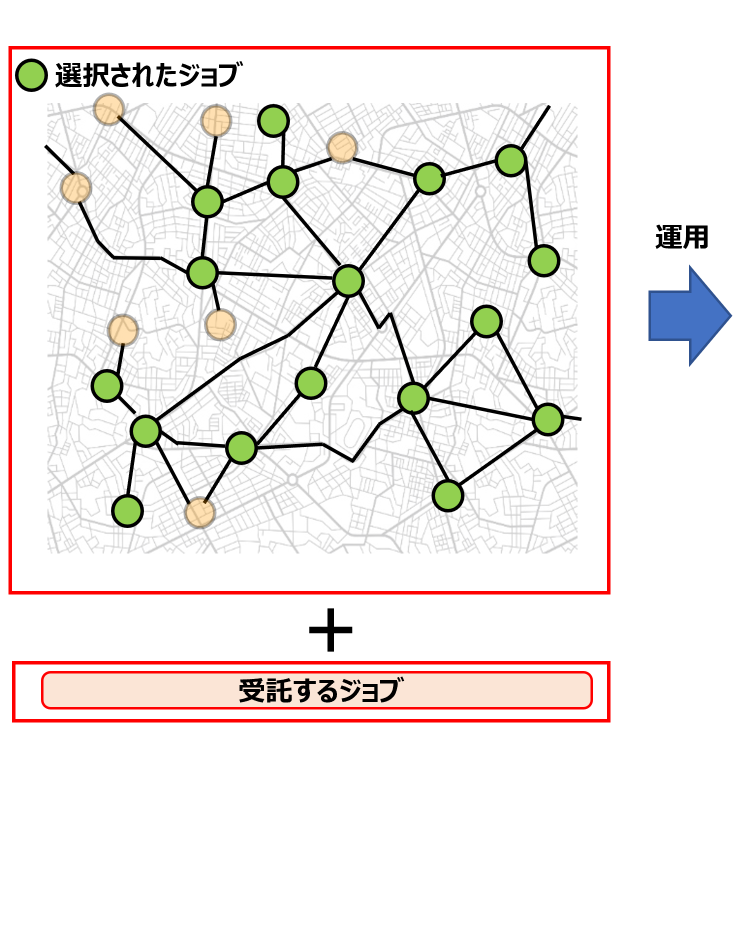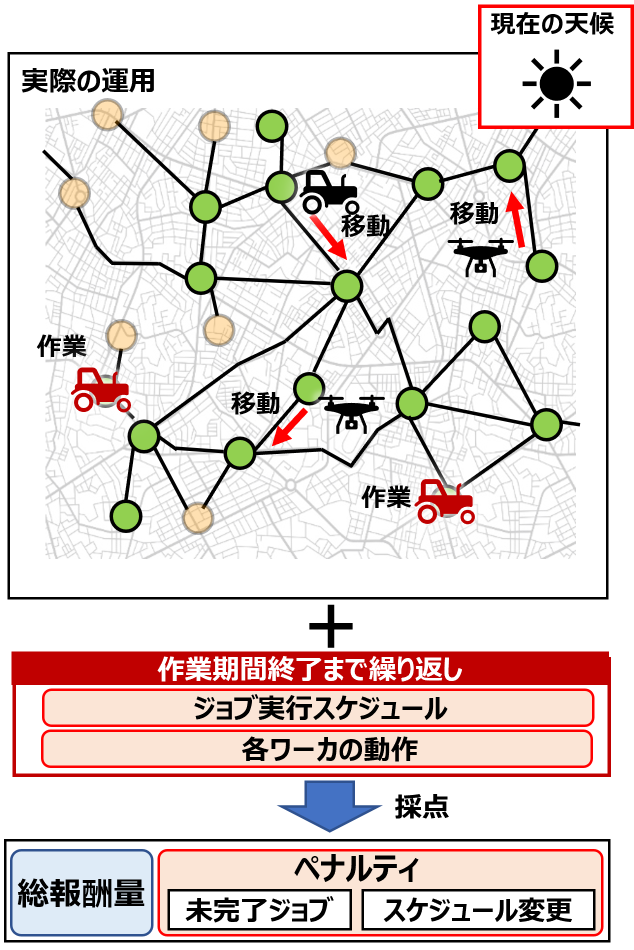    入力として最初に以下の情報が与えられる。 1. 作業期間 2. 地理情報（グラフ） 3. ワーカーの情報 4. 全てのジョブの情報 5. 天候に関する情報 6. スケジュールに関する情報 これに対し最初にコンテスタントは 1. 受託するジョブ を出力する。 以降各時刻開始時に入力として以下の情報が与えられる。 1. 受託したジョブに関する情報 2. ワーカーの現在位置 3. (一定間隔で)天候の予報 これに対しコンテスタントは 1. ジョブ実行スケジュール 2. 各ワーカーの動作 を出力する。これを作業期間終了まで繰り返す。 スコアは 1. 報酬 2. 未完了ジョブに対するペナルティ 3. スケジュール変更の度合い・スケジュール遵守の度合い を考慮して採点される。 以下はその詳細である。 ### 入力1 最初に入力として 1. 作業期間 2. 地理情報（グラフ） 3. ワーカーの情報 4. 全てのジョブの情報 5. 天候に関する情報 6. スケジュールに関する情報 が以下の形式で標準入力から与えられる。 > $ T_{\rm{max}}\\ N_V\,\,N_E\\ u_1\quad\ v_1\quad\ d_1\\ \vdots\\ u_{N_E}\,\,\ v_{N_E}\,\,\ d_{N_E}\\ N_{\rm{worker}}\\ v^{\rm{init}}_1\,\,L^\text{max}_1\,\,N^{\rm{JobType}}_1\,\,\text{Type}^1_1\,\,\text{Type}^1_2\,\,\cdots\ \text{Type}^1_{N^{\rm{JobType}}_1}\\ \vdots\\ v^{\rm{init}}_{N_{\rm{worker}}}\,\,L^\text{max}_{N_{\rm{worker}}}\,\,N^{\rm{JobType}}_{N_{\rm{worker}}}\,\,\text{Type}^{N_{\rm{worker}}}_1\,\,\text{Type}^{N_{\rm{worker}}}_2\,\,\cdots\ \text{Type}^{N_{\rm{worker}}}_{N^{\rm{JobType}}_1}\\ N_{\rm{job}}\\ \text{Job}_1\\ \vdots\\ \text{Job}_{N_{\rm{job}}}\\ T^{\rm{weather}}\,\,N^{\rm{weather}}\\ \begin{array}{llll} p^{\rm{weather}}_{1,1}\ &\ p^{\rm{weather}}_{1,2}\ &\ \cdots\ &\ p^{\rm{weather}}_{1,N^{\rm{weather}}}\\ p^{\rm{weather}}_{2,1}\ &\ p^{\rm{weather}}_{2,2}\ &\ \cdots\ &\ p^{\rm{weather}}_{2,N^{\rm{weather}}}\\ \vdots\ &\ \vdots\ &\ \ddots\ &\ \vdots\\ p^{\rm{weather}}_{N^{\rm{weather}},1}\ &\ p^{\rm{weather}}_{N^{\rm{weather}},2}\ &\ \cdots\ &\ p^{\rm{weather}}_{N^{\rm{weather}},N^{\rm{weather}}}\\ \end{array}\\ c_1\,\,c_2\,\,\cdots\,\,c_{N^{\rm{weather}}}\\ P_m\,\,\ R_m\,\,\ \alpha\\ t_1\,\,\ p^1_1\,\,\ p^1_2\,\,\ \cdots\ \,\,\ p^1_{N^{\rm{weather}}}\\ t_2\,\,\ p^2_1\,\,\ p^2_2\,\,\ \cdots\ \,\,\ p^2_{N^{\rm{weather}}}\\ \vdots\\ t_{N'}\,\,\ p^{N'}_1\,\,\ p^{N'}_2\,\,\ \cdots\ \,\,\ p^{N'}_{N^{\rm{weather}}} $ ($ \text{Job}_i $の構成は後述) #### 作業期間 - **入力** - 最初の$ 1 $行目で作業期間の長さ$ T_\text{max} $が与えられる。 この問題における時刻$ t $は $ 1 $ から $ T_{\text{max}} $までの整数の値をとる。 入力例 以下は $ T_\text{max}=300 $の例: ``` 300 ``` (末尾に改行有) - 1行目:作業期間の長さは`300` である。($ T_\text{max}=300 $) #### 地理情報 - **入力** - 次の$ 1 $行で、問題の地理情報を表すグラフ(連結な正の重み付き無向グラフ)の頂点数$ N_V $と辺の数$ N_E $が与えられる。 - この$ N_V $個の頂点には$ 1 $から順に$ N_V $まで頂点番号が割り当てられるものとする。 - 続く$ N_E $行で辺を表す情報: 端点$ u_i,v_i $と重み(=距離)$ d_i $ が与えられる。($ 1\leq\ i\ \leq\ N_E $) 後述するが、[ジョブ](#job)はこのグラフの頂点上に配置され、[ワーカー](#worker)はこのグラフの上を移動する。 入力例 以下は $ N_V=14,N_E=19 $の例: ``` 14 19 1 7 1 1 2 1 2 9 1 2 3 1 3 5 1 3 7 1 3 6 1 4 13 2 4 10 2 4 6 1 4 5 1 6 8 1 7 8 1 8 14 2 9 11 2 10 12 2 10 11 2 12 13 2 13 14 2 ``` (末尾に改行有) - 1行目:グラフの頂点は`14`個存在し、辺は`19`個存在する。($ N_V=14,N_E=19 $) - この`14`個の頂点には$ 1 $から順に`14`まで頂点番号が割り当てられている。 - 以下、頂点番号$ i $に対応する頂点 を単に 頂点$ i $ と呼ぶ。 - 2行目:頂点`1`と頂点`7`の間に長さ`1`の辺が存在する。($ u_{1}=1,v_{1}=7,d_{1}=1 $) - 3行目:頂点`1`と頂点`2`の間に長さ`1`の辺が存在する。($ u_{2}=1,v_{2}=2,d_{2}=1 $) - 4行目:頂点`2`と頂点`9`の間に長さ`1`の辺が存在する。($ u_{3}=2,v_{3}=9,d_{3}=1 $) - 5行目:頂点`2`と頂点`3`の間に長さ`1`の辺が存在する。($ u_{4}=2,v_{4}=3,d_{4}=1 $) - 6行目:頂点`3`と頂点`5`の間に長さ`1`の辺が存在する。($ u_{5}=3,v_{5}=5,d_{5}=1 $) - 7行目:頂点`3`と頂点`7`の間に長さ`1`の辺が存在する。($ u_{6}=3,v_{6}=7,d_{6}=1 $) - 8行目:頂点`3`と頂点`6`の間に長さ`1`の辺が存在する。($ u_{7}=3,v_{7}=6,d_{7}=1 $) - 9行目:頂点`4`と頂点`13`の間に長さ`2`の辺が存在する。($ u_{8}=4,v_{8}=13,d_{8}=2 $) - 10行目:頂点`4`と頂点`10`の間に長さ`2`の辺が存在する。($ u_{9}=4,v_{9}=10,d_{9}=2 $) - 11行目:頂点`4`と頂点`6`の間に長さ`1`の辺が存在する。($ u_{10}=4,v_{10}=6,d_{10}=1 $) - 12行目:頂点`4`と頂点`5`の間に長さ`1`の辺が存在する。($ u_{11}=4,v_{11}=5,d_{11}=1 $) - 13行目:頂点`6`と頂点`8`の間に長さ`1`の辺が存在する。($ u_{12}=6,v_{12}=8,d_{12}=1 $) - 14行目:頂点`7`と頂点`8`の間に長さ`1`の辺が存在する。($ u_{13}=7,v_{13}=8,d_{13}=1 $) - 15行目:頂点`8`と頂点`14`の間に長さ`2`の辺が存在する。($ u_{14}=8,v_{14}=14,d_{14}=2 $) - 16行目:頂点`9`と頂点`11`の間に長さ`2`の辺が存在する。($ u_{15}=9,v_{15}=11,d_{15}=2 $) - 17行目:頂点`10`と頂点`12`の間に長さ`2`の辺が存在する。($ u_{16}=10,v_{16}=12,d_{16}=2 $) - 18行目:頂点`10`と頂点`11`の間に長さ`2`の辺が存在する。($ u_{17}=10,v_{17}=11,d_{17}=2 $) - 19行目:頂点`12`と頂点`13`の間に長さ`2`の辺が存在する。($ u_{18}=12,v_{18}=13,d_{18}=2 $) - 20($ =1+N_E $)行目:頂点`13`と頂点`14`の間に長さ`2`の辺が存在する。($ u_{19}=13,v_{19}=14,d_{19}=2 $) #### ワーカー ワーカーはジョブを処理する存在であり、移動とタスクの実行が可能である。これはコンテスタントの入力により操作される。([ワーカーの行動](#worker-action)を参照) - **入力** - 続く$ 1 $行でワーカーの数$ N_{\text{worker}} $が与えられる。 - 次の$ N_{\text{worker}} $行で各ワーカーの構成情報: - 初期位置(頂点番号): $ v^{\text{init}}_i $ - 単位時間に実行可能なタスク数の上限: $ L^{\text{max}}_i $ - 実行可能なジョブのタイプ数 $ N^{\text{JobType}}_i $ と タイプの列 $ \text{Type}^i_1\,\,\text{Type}^i_2\,\,\cdots\,\,\text{Type}^i_{N^{\text{JobType}}_i} $ が与えられる。($ 1\leq\ i\ \leq\ N_{\text{worker}} $) この入力における順序はワーカーのIDに対応する。 ワーカーごとに、単位時間に実行可能なタスク数の上限 や 処理できるジョブのタイプは異なる。また、実際に実行可能なタスク数は天候により左右される。 入力例 以下は $ N_{\text{worker}}=5 $ の例: ``` 5 6 100 3 1 2 3 13 59 1 3 10 55 2 2 3 9 47 3 1 2 3 9 89 1 2 ``` (末尾に改行有) - 1行目:ワーカーの数は`5`である。($ N_{\text{worker}}=5 $) - 2行目:ID=1であるワーカーの記述。 - 初期位置は頂点番号`6`に対応する頂点である。($ v^{\text{init}}_1=6 $) - 単位時間あたりに実行可能なタスク数の上限は`100`である。($ L^{\text{max}}_1=100 $) - 実行可能なジョブのタイプは`3`つあり($ N^{\text{JobType}}_1=3 $)、それらは`1`と`2`と`3`である。($ \text{Type}^1_1=1,\text{Type}^1_2=2,\text{Type}^1_3=3 $) - 3行目:ID=2であるワーカーの記述。 - 初期位置は頂点番号`13`に対応する頂点である。($ v^{\text{init}}_2=13 $) - 単位時間あたりに実行可能なタスク数の上限は`59`である。($ L^{\text{max}}_2=59 $) - 実行可能なジョブのタイプは`1`つあり($ N^{\text{JobType}}_2=1 $)、それは`3`である。($ \text{Type}^2_1=3 $) - 4行目:ID=3であるワーカーの記述。 - 初期位置は頂点番号`10`に対応する頂点である。($ v^{\text{init}}_3=10 $) - 単位時間あたりに実行可能なタスク数の上限は`55`である。($ L^{\text{max}}_3=55 $) - 実行可能なジョブのタイプは`2`つあり($ N^{\text{JobType}}_3=2 $)、それらは`2`と`3`である。($ \text{Type}^3_1=2,\text{Type}^3_2=3 $) - 5行目:ID=4であるワーカーの記述。 - 初期位置は頂点番号`9`に対応する頂点である。($ v^{\text{init}}_4=9 $) - 単位時間あたりに実行可能なタスク数の上限は`47`である。($ L^{\text{max}}_4=47 $) - 実行可能なジョブのタイプは`3`つあり($ N^{\text{JobType}}_4=3 $)、それらは`1`と`2`と`3`である。($ \text{Type}^4_1=1,\text{Type}^4_2=2,\text{Type}^4_3=3 $) - 6($ =1+N_{\text{worker}} $)行目:ID=5であるワーカーの記述。 - 初期位置は頂点番号`9`に対応する頂点である。($ v^{\text{init}}_5=9 $) - 単位時間あたりに実行可能なタスク数の上限は`89`である。($ L^{\text{max}}_5=89 $) - 実行可能なジョブのタイプは`1`つあり($ N^{\text{JobType}}_5=1 $)、それは`2`である。($ \text{Type}^5_1=2 $) #### ジョブ ジョブは頂点上でワーカーが実行する仕事である。 - **ジョブとは** - **ジョブ**は現実における作業の1つの単位に相当し、例えば作物の収穫や農薬の散布等である。 - これらはより小さな単位の複数作業から構成される。例えば、果実1つを摘み取る、稲を一定面積刈り取る、農薬を一定面積に撒く、といったものである。このようにジョブを構成する小さな単位の作業をここでは**タスク**と呼ぶことにする。 - ジョブを構成するタスクが全て一定量行われることでそのジョブは完了すると考える。 - 現実的にはジョブは複数種類のタスクから構成されるかもしれないが、今回は単純化しタスクをこなす量だけに着目する。すなわち、**タスクを規定の量処理することでジョブが完了したとみなす**ことにする。 - ジョブが行われる場所はそのジョブ毎に異なる。この問題ではそれを[地理情報](#geo-data)として与えられた**グラフの頂点上にジョブを配置**することで表現する。 - **タスクの処理と報酬** - 各ジョブのタスクを処理するものとして**[ワーカー](#worker)**が存在する。 - コンテスタントは各ワーカーに**移動**や**作業**の指示を出し、ジョブが存在する頂点に移動させタスクを処理する。 - コンテスタントは**ジョブを完了する(=タスクを規定の量処理する)ことで報酬を得る**。 - ワーカーは単位時間あたりに処理できるタスク量に上限([実行タスク数制限](#task-limit))があり、ジョブを完了するにはある程度時間がかかる。典型的には、ある時刻から一定時間、毎時刻タスクを一定量処理することになる。 - **ジョブ完了時に得られる報酬はタスクを処理した時刻によって異なる**。具体的には:各時刻におけるタスク処理量あたりの報酬量$ r(t) $ $ \times $ その時刻に処理されたタスク量 の時間に関する総和($ t=1,2,\cdots,T_\text{max} $)である。 - 各時刻におけるタスク処理量あたりの報酬量$ r(t) $は**ジョブ毎にも異なる。** - 全ワーカーが集めた報酬の総和がこの問題のスコアを構成する中心的な要素である。([採点方法](#scoring-method)) コンテスタントはこの報酬の総和が大きくなるように、他の要素も考慮しつつワーカーの行動を決定する。 - **ジョブ間の依存関係** - ジョブは他のジョブに依存する場合がある。すなわち、そのジョブが依存するジョブが全て完了していなければそのジョブのタスクを処理することができないという制限がある。 - 依存するジョブが存在しない場合このような制限は無い。 - **ジョブの受託** - コンテスタントは**問題開始時に受託するジョブを選択する**。([出力1](#output1)) - **受託が必須であるジョブが存在する**ため、それらを全て含むようにジョブを選択する。 - 受託したジョブが未完了のまま作業期間を終えた場合、ジョブ毎に指定された**未完了ペナルティが発生する。** 各種制限- 報酬が獲得できない時刻(タスク処理量あたりの報酬量 = 0 である時刻)にはタスクを処理することができない。 \- ワーカーの単位時間当たりのタスク実行数上限は天候に影響される。([実行タスク数制限](#task-limit)) \- 受託していないジョブは実行できない。 - **入力** - 続く$ 1 $行でジョブの数$ N_{\text{job}} $が与えられる。 - 次の行からジョブの構成情報$ \text{Job}_i $が$ N_{\text{job}} $個与えられる。(合計$ N_{\text{job}}\times\ 3 $行) ジョブの構成情報$ \text{Job}_i $は次の形式で与えられる。 > $ \text{ID}^{\rm{job}}_i\,\,\text{Type}_i\,\,N^{\rm{task}}_i\,\,v^{\rm{job}}_i\,\,\ P^{\rm{job}}_i\,\,d^\text{weather}_i\,\,\ f^{\rm{mandatory}}_i\\ N^{\rm{reward}}_i\,\,\ t^{\rm{reward}}_{i,1}\,\,\ y^{\rm{reward}}_{i,1}\cdots\ t^{\rm{reward}}_{i,N^{\rm{reward}}_i}\,\,\ y^{\rm{reward}}_{i,N^{\rm{reward}}_i}\\ N^{\rm{depend}}_i\,\,\ {\rm{id}}^{\rm{depend}}_{i,1}\,\,\ \cdots\ \,\,{\rm{id}}^{\rm{depend}}_{i,N^{\rm{depend}}_i} $ - 1行目 - ジョブID: $ \text{ID}^{\text{job}}_i $ - ジョブタイプ: $ \text{Type}_i $ - 完了までのタスク数: $ N^{\text{task}}_i $ - ジョブの位置(頂点番号): $ v^{\text{job}}_i $ - ジョブを受託したが完了しなかった場合のペナルティ係数: $ P^{\text{job}}_i $ - 天候依存度: $ d^\text{weather}_i $ - 受託必須ジョブフラグ: $ f^{\text{mandatory}}_i $ ($ 0 $:必須でない、$ 1 $:必須) - 2行目(報酬関数$ r(t) $の定義) - 報酬関数の制御点個数:$ N^{\text{reward}}_i $ - 制御点の列:$ t^{\rm{reward}}_{i,1}\,\,y^{\rm{reward}}_{i,1}\,\,t^{\rm{reward}}_{i,2}\,\,y^{\rm{reward}}_{i,2}\,\,\cdots\,\,t^{\rm{reward}}_{i,N^{\text{reward}}_i}\,\,y^{\rm{reward}}_{i,N^{\text{reward}}_i} $ - 3行目(依存するジョブ) - 依存するジョブの数: $ N^{\text{depend}}_i $ - 依存するジョブID: $ {\rm{id}}^{\rm{depend}}_{i,1}\,\,{\rm{id}}^{\rm{depend}}_{i,2}\,\,\ \cdots\ \,\,{\rm{id}}^{\rm{depend}}_{i,N^{\rm{depend}}_i} $ 報酬関数$ r(t) $の詳細 時刻$ t $におけるタスク当たりの報酬を与える関数$ r(t) $は、1個以上の制御点(時刻と値のペア)とそれらの間の線形補間で定める。 すなわち、制御点の列$ p=((t_i,y_i))_{i=1,\cdots,n} $ ($ t_i,y_i\in\ \mathbb{Z},t_1\ $ N_\text{schedule}\\ \text{id}_1\,\,\text{id}_2\,\,\cdots\,\,\text{id}_{N_\text{schedule}}\\ \text{job}^{\text{id}_1}_t\,\,\text{job}^{\text{id}_1}_{t+1}\,\,\cdots\,\,\text{job}^{\text{id}_1}_{T_\text{max}}\\ \vdots\\ \text{job}^{\text{id}_{N_\text{schedule}}}_t\,\,\text{job}^{\text{id}_{N_\text{schedule}}}_{t+1}\,\,\cdots\,\,\text{job}^{\text{id}_{N_\text{schedule}}}_{T_\text{max}}\\ {\rm{action}}_1\\ {\rm{action}}_2\\ \vdots\\ {\rm{action}}_{N_{\rm{worker}}} $ (末尾に改行を挿入すること) #### スケジュールの提出 各ワーカーは、"各時刻におけるジョブID"の列をジョブ実行スケジュールとして保持している。 コンテスタントは時刻$ t=1 $に全ワーカーのスケジュールを提出する。以後どの時刻でも、変更が必要なワーカーのみ選択して再提出しスケジュールを変更することができる。 - **出力** - 最初の$ 1 $行で、スケジュールを変更するワーカーの数$ N_\text{schedule} $を出力する。 - 続く$ 1 $行で、ワーカーのIDの列$ \text{id}_1\,\,\text{id}_2\,\,\cdots\,\,\text{id}_{N_\text{schedule}} $を出力する。 - 続く$ N_\text{schedule} $行で、ワーカー(ID=$ \text{id}_i $)の現在時刻$ t $から$ T_\text{max} $までのスケジュール(各時刻で行うジョブのID) $ \text{job}^{\text{id}_i}_t\,\,\text{job}^{\text{id}_i}_{t+1}\,\,\cdots\,\,\text{job}^{\text{id}_i}_{T_\text{max}} $を出力する。($ 1\leq\ i\ \leq\ N_\text{schedule} $) - 以下の条件を満たさない場合`WA`(Wrong Answerとなる) - $ N_\text{schedule}\ \geq\ 0 $ - ワーカーIDの列の長さは$ N_\text{schedule} $である。 - 指定されたワーカーID全てについて、対応するワーカーが存在する。 - ワーカーIDは重複していない。 - 提出時刻を$ t $とすると、スケジュールで指定されるジョブIDの数は$ T_\text{max}-t+1 $である。 - 時刻$ t=1 $の場合のみ: $ N_\text{schedule}\ =\ N_\text{worker} $ スケジュールの再提出を行うと、既存のスケジュールからの変更の大きさに依存してスケジュール加点量が減少する。([スケジュール加点](#schedule-added-point)を参照) #### ワーカーの行動 コンテスタントは全てのワーカーの行動$ \text{action} $を毎時刻指定する。$ \text{action} $の実体は文字列であり、以下の3種類のいずれかである。 - `stay`:移動もジョブ実行もせずその場にとどまる。 - `move w`:現在位置から頂点番号`w`に対応する頂点の方向にその間の最短経路上を距離$ 1 $だけ進む。以下の条件を満たさない場合`WA`(Wrong Answer)となる。 - 頂点番号`w`に対応する頂点は存在する。 - 現在位置と頂点番号`w`に対応する頂点は異なる。 - `execute i a`:ID=`i`のジョブをタスク数`a`だけ実行する。ただし、以下の条件を満たさない場合`WA`(Wrong Answer)となる。 - 受託したジョブの中にID=`i`であるものが存在する。 - ワーカーの現在位置とID=`i`であるジョブが存在する頂点が一致する。 - ID=`i`のジョブのタイプは、このワーカーの実行可能ジョブタイプに含まれる。 - `a`は1以上の整数。 - `a`はID=`i`のジョブの残タスク数を超えない。 - `a`は実行タスク数制限を超えない。(詳細は[実行タスク数制限](#task-limit)) - ID=`i`のジョブが依存するジョブは全て完了している。 - 報酬の値は正である。 `move w`に関して、現在位置と頂点`w`の間に2つ以上の異なる最短経路が存在する場合どれが選ばれるかは未規定である。そのような場合でも、コンテスタントは経路の途中の点を指定して移動する操作を繰り返すことで希望の経路を選ぶことができる。 上記のいずれの文字列パターンにも合致しない$ \text{action} $が指定された場合`WA`(Wrong Answer)となる。 また、各時刻終了時に、合計タスク処理量 が 完了までのタスク数 $ N^{\text{task}}_i $ を超えるようなジョブが存在する場合 `WA` または `RE` となる。 - **出力** - 次の$ N_\text{worker} $行で各ワーカーの行動$ \text{action}_i $を出力する。($ 1\ \leq\ i\ \leq\ N_\text{worker} $) 出力が有効であれば[入力2](#input2)に進み次の時刻を開始する。現在時刻が$ T_\text{max} $ならば[入力3(採点)](#input3)に進む。 出力例 以下は$ N_\text{worker}=3,T_\text{max}=10 $の例である。 #### 例1:行動+初期スケジュール提出($ t=1 $) ``` 3 1 2 3 85 85 85 85 431 431 431 431 431 431 65 65 65 65 65 65 65 65 65 65 730 730 639 639 639 639 4 4 4 4 execute 85 135 move 12 move 98 ``` - 1行目:コンテスタントは`3`つのワーカーのスケジュールを提出する。 - 2行目:対象となるワーカーはID=`1`,`2`,`3`のものである。 - 3行目:これは2行目で1番目に指定されたワーカー(ID=`1`)のスケジュールであり、以下の通りである: - 時刻$ 1 $でID=`85`のジョブを実行する。同様に、時刻$ 2 $でID=`85`、時刻$ 3 $でID=`85`、時刻$ 4 $でID=`85`、時刻$ 5 $でID=`431`、時刻$ 6 $でID=`431`、時刻$ 7 $でID=`431`、時刻$ 8 $でID=`431`、時刻$ 9 $でID=`431`、時刻$ 10 $でID=`431`のジョブを処理する。 - 4行目:これは2行目で2番目に指定されたワーカー(ID=`2`)のスケジュールであり、以下の通りである: - 時刻$ 1 $でID=`65`のジョブを実行する。同様に、時刻$ 2 $でID=`65`、時刻$ 3 $でID=`65`、時刻$ 4 $でID=`65`、時刻$ 5 $でID=`65`、時刻$ 6 $でID=`65`、時刻$ 7 $でID=`65`、時刻$ 8 $でID=`65`、時刻$ 9 $でID=`65`、時刻$ 10 $でID=`65`のジョブを処理する。 - 5行目:これは2行目で3番目に指定されたワーカー(ID=`3`)のスケジュールであり、以下の通りである: - 時刻$ 1 $でID=`730`のジョブを実行する。同様に、時刻$ 2 $でID=`730`、時刻$ 3 $でID=`639`、時刻$ 4 $でID=`639`、時刻$ 5 $でID=`639`、時刻$ 6 $でID=`639`、時刻$ 7 $でID=`4`、時刻$ 8 $でID=`4`、時刻$ 9 $でID=`4`、時刻$ 10 $でID=`4`のジョブを処理する。 - 6行目:現在時刻におけるID=1のワーカーの行動を次のように指定する:ID=`85`のジョブのタスクを`135`だけ処理する。 - 7行目:現在時刻におけるID=2のワーカーの行動を次のように指定する:頂点`12`に向かって移動する。 - 8行目:現在時刻におけるID=3のワーカーの行動を次のように指定する:頂点`98`に向かって移動する。 #### 例2:行動+スケジュールを変更しない ``` 0 stay move 87 execute 670 40 ``` - 1行目:コンテスタントは`0`個のワーカーのスケジュールを提出する。(=スケジュールを変更しない) - 2行目:対象となるワーカーは存在しない。（=ワーカーIDが0個入った行、すなわち空行が入る） - （存在しない行:0個のワーカーに対してスケジュールが出力され、合計0行出力される。） - 3行目:現在時刻におけるID=1のワーカーの行動を次のように指定する:何もしない - 4行目:現在時刻におけるID=2のワーカーの行動を次のように指定する:頂点`87`に向かって移動する。 - 5行目:現在時刻におけるID=3のワーカーの行動を次のように指定する:ID=`670`のジョブのタスクを`40`だけ処理する。 #### 例3:行動+スケジュール変更($ t=6 $) ``` 2 2 3 65 65 65 65 223 639 4 4 91 91 execute 431 80 execute 65 40 move 9 ``` - 1行目:コンテスタントは`2`個のワーカーのスケジュールを提出(変更)する。 - 2行目:対象となるワーカーはID=`2`,`3`のものである。 - 3行目:これは2行目で1番目に指定されたワーカー(ID=`2`)の(変更された)スケジュールであり、以下の通りである: - 時刻$ 6 $でID=`65`のジョブを実行する。同様に、時刻$ 7 $でID=`65`、時刻$ 8 $でID=`65`、時刻$ 9 $でID=`65`、時刻$ 5 $でID=`223`のジョブを処理する。 - 4行目:これは2行目で2番目に指定されたワーカー(ID=`3`)の(変更された)スケジュールであり、以下の通りである: - 時刻$ 6 $でID=`639`のジョブを実行する。同様に、時刻$ 7 $でID=`4`、時刻$ 8 $でID=`4`、時刻$ 9 $でID=`91`、時刻$ 5 $でID=`91`のジョブを処理する。 - 5行目:現在時刻におけるID=1のワーカーの行動を次のように指定する:ID=`431`のジョブのタスクを`80`だけ処理する。 - 6行目:現在時刻におけるID=2のワーカーの行動を次のように指定する:ID=`65`のジョブのタスクを`40`だけ処理する。 - 7行目:現在時刻におけるID=3のワーカーの行動を次のように指定する:頂点`9`に向かって移動する。 ### 入力3(採点) 時刻$ t=T_\text{max} $の[出力2](output2)終了後、出力が有効であれば、入力としてスコア$ S $を標準入力から以下の形式で与える。 > $ S $ この値を入力から受け取らない場合、`TLE`となる可能性がある。 また、順位付けに関しては [順位決定方法](#ranking-method) を参照せよ。 #### 採点方法 スコア$ S $は総報酬量$ R $、未完了ペナルティ$ U $、スケジュール加点$ A $から以下の式により決定される。 $ S=\left\lfloor\ R\ \times\ U\ \times\ (1+\alpha\ A)\ \right\rfloor $ ただし、$ \left\lfloor\ x\ \right\rfloor $ は$ x $を超えない最大の整数を返す関数(床関数)である。 $ ~ $ $ R,U,A $の計算式は以下の通りである。 **総報酬量$ R $**: $ \begin{aligned} R=\sum_{j\in\ J_\text{finished}}\sum_{w\ \in\ W}\sum_{t=1}^{T_\text{max}}a^w_j(t)r_j(t) \end{aligned} $ - 完了したジョブの集合:$ J_\text{finished} $ - 全ワーカーの集合:$ W $ - 時刻$ t $にワーカー$ w $が実行したジョブ$ j $のタスク数:$ a^w_j(t) $ - 時刻$ t $におけるジョブ$ j $のタスク当たりの報酬:$ r_j(t) $ **未完了ペナルティ$ U $**: $ \begin{aligned} U=\prod_{j\ \in\ J_{\text{unfinished}}}\ P^{\text{job}}_j \end{aligned} $ - 受託したが未完了であるジョブの集合:$ J_\text{unfinished} $ - ジョブ$ j $の未完了ペナルティ係数:$ P_j^\text{job} $ **スケジュール加点$ A $**: $ A $は初期値を$ 1.0 $として毎時刻以下の規則で更新される: - 各ワーカーに対して: - スケジュールと異なるジョブを実行した場合: $ \begin{aligned}A\leftarrow\ 0\end{aligned} $ - スケジュールと同じジョブを実行した場合: $ \begin{aligned}A\leftarrow\ A\end{aligned} $ - ジョブを実行しなかった場合: $ \begin{aligned}A\leftarrow\ A\end{aligned} $ - 各ワーカーのスケジュール再提出について、提出時刻を$ t $とすると: - 時刻$ s(\geq\ t) $のジョブIDについて: - 変更する場合: $ \begin{aligned}A\leftarrow\ A\times\ \left(1.0-P_m\ \times\ (R_m)^{s-t}\right)\end{aligned} $ - 変更しない場合: $ \begin{aligned}A\leftarrow\ A\end{aligned} $ ただし、初期スケジュール提出時には$ A $の更新は行われない。 空集合に対する総和$ \sum $は$ 0 $であり、空集合に対する総乗$ \prod $は$ 1 $である。 ### 実行タスク数制限 ワーカーが1単位時間に処理できるタスクの最大量は、**ワーカーの最大タスク実行数$ L^\text{max} $**、と処理対象のジョブの**天候依存度$ d^\text{weather} $**、**天候**$ w\ \in\ \{1,\cdots,N_\text{weather}\} $により以下のように決定される: $ \begin{aligned} L^\text{max}\times\ (1-d^\text{weather})^{c_w}\end{aligned} $ ただし、$ c_w $は[入力1](#input1)で与えられた制限定数に対応する。また、ここでは$ 0^0=1 $と定める。 ### テストケース生成規則 地理情報(グラフ) - 用語 - 矩形領域$ [x_0,x_1]\times[y_0,y_1]\,\,(x_0\ \ 0 $ - 切断面積比:$ C\in\ (0,1] $ - **生成手順1**(グラフの